Vận dụng trang 20 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST

Hướng dẫn giải

+) Biểu diễn: \(A \subset B\)

+) Sau đó, biểu diễn: \(B \subset C\)

+) Quan sát biểu đồ Ven, đưa ra kết luận

Lời giải chi tiết

Khẳng định của bạn An là đúng.

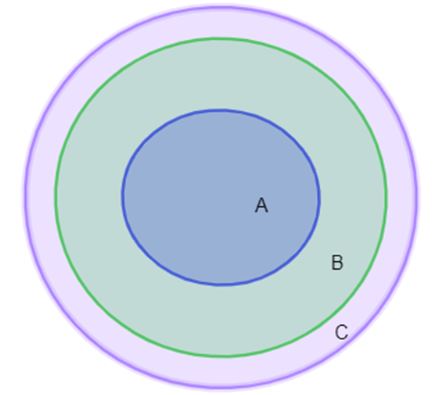
Thật vậy, ta có sơ đồ ven sau:

Dựa vào sơ đồ ta thấy tập hợp A nằm trong tập hợp B và tập hợp B nằm trong tập hợp C. Do đó tập hợp A nằm hoàn toàn trong tập hợp C hay tất cả phần tử của tập hợp A đều thuộc tập hợp C.

Suy ra A ⊂ C.

-- Mod Toán 10 HỌC247