Một tấm nhôm mỏng, trên có rạch hai khe hẹp song song ${S_1}$ và ${S_2}$ và đặt cách một màn 1,2 m. Đặt giữa màn và hai khe một thấu kính hội tụ có tiêu cự $\frac{{80}}{3}cm$, người ta tìm được hai trị trí của thấu kính cho ảnh của hai khe ${S_1}$ và ${S_2}$ rõ nét trên màn. Ở vị trí mà ảnh lớn hơn thì khoảng cách giữa hai ảnh ${S_1}'$ và ${S_2}'$ là 1,6mm. Khi bỏ thấu kính ra và chiếu sáng hai khe bằng ánh sáng đơn sắc có bước sóng $0,6\mu m$ thì khoảng vân giao thoa trên màn là

Đáp án : B

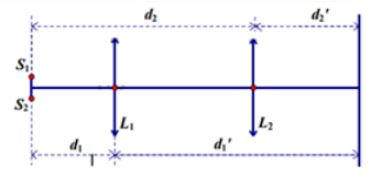
Trên hình vẽ, ta có ${L_1};{L_2}$ là 2 vị trí của thấu kính sao cho ảnh rõ nét của 2 nguồn trên màn.

Gọi $f$ là tiêu cự của thấu kính, ta có:

+ Xét vị trí ${L_1}$: $\frac{1}{f} = \frac{1}{{{d_1}}} + \frac{1}{{d{'_1}}}$

+ Xét vị trí ${L_2}$: $\frac{1}{f} = \frac{1}{{{d_2}}} + \frac{1}{{d{'_2}}}$

$\Rightarrow \frac{1}{{{d_1}}} + \frac{1}{{{d_1}'}} = \frac{1}{{{d_2}}} + \frac{1}{{{d_2}'}}$

Lại có: ${d_1} + {d_1}' = {d_2} + {d_2}' = S$

$\Rightarrow {d_1}.{d_1}' = {d_2}{d_2}' = P\,\,\,\,\,\left( 1 \right)$

Từ (1) ta suy ra ${d_1};{d_1}'$ là 2 nghiệm của phương trình:

${X^2} - S{\rm{X}} + P = 0$ và ${d_2};{d_2}'$ cũng vậy.

Phương trình trên là phương trình bậc 2 có 2 nghiệm phân biệt ${X_1},{X_2}$

Do ${d_1} \ne {d_2}$ nên ${X_1} = {d_1} = {d_2}'$ và ${X_2} = {d_2} = {d_1}'$

Theo đề bài ta có:

$\left\{ \begin{array}{l}{d_1} + {d_1}' = 1,2m = 120cm\\\frac{3}{{80}} = \frac{1}{{{d_1}}} + \frac{1}{{120 - {d_1}}}\end{array} \right. \Rightarrow \left\{ \begin{array}{l}{d_1} = {d_2}' = 40cm\\{d_1}' = {d_2} = 80cm\end{array} \right.$

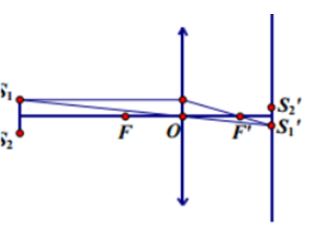
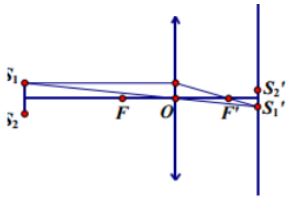
Ta xét 1 vị trí bất kì của thấu kính

Từ hình vẽ, ta có: ${S_1}'{S_2}' = {S_1}{S_2}\frac{{d'}}{d}$

Suy ra để có ảnh lớn hơn, ta phải có $\frac{{d'}}{d} > 1$

Tức là thấu kính gần ${S_1}{S_2}$ hơn

Khi đó: $\left\{ \begin{array}{l}d = 40cm\\d' = 80cm\end{array} \right.$

$\Rightarrow {S_1}{S_2} = {S_1}'{S_2}'\frac{d}{{d'}} = 1,6\frac{{40}}{{80}} = 0,8mm$

Vậy $a = 0,8mm$

Khi bỏ thấu kính cho giao thoa ánh sáng trên màn khi đó có khoảng vân:

$i = \frac{{\lambda D}}{a} = \frac{{0,{{6.10}^{ - 6}}.1,2}}{{0,{{8.10}^{ - 3}}}} = {9.10^{ - 4}}m = 0,9mm$