-
Câu hỏi:
Li độ của một vật dao động điều hòa có biểu thức Độ dài quãng đường mà vật đi được trong khoảng thời gian 8/3s tính từ thời điểm ban đầu là:
Chu kỳ:
Ban đầu: t = 0 ⇒ x = - A = -8 cm
Ta có:
Sau 2 T vật đi được quãng đường: S1 = 2.4.A = 64 cm
Sau vật đi được quảng đường;
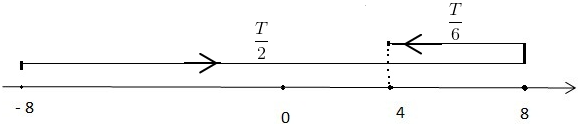
Quãng đường vật đi được là: S = S1 + S2 = 84 cmYOMEDIA
Hướng dẫn Trắc nghiệm Online và Tích lũy điểm thưởng
CÂU HỎI KHÁC VỀ DAO ĐỘNG ĐIỀU HÒA
- Một vật dao động điều hòa với phương trình (x = 10 cos(5 pi t - pi / 2)). Tính quãng đường vật đi được trong khoảng thời gian 1,55s
- Một vật dao động điều hoà với phương trình (x = A cos( omega t + frac{pi}{3})). Giá trị của A và w là
- Quả cầu của con lắc lò xo dao động điều hòa theo phương trình (x = 4 cos ( pi t - frac{pi}{2}) cm
- Một vật dao động điều hòa với phương trình (x = 6 cos(4 pi t + frac{pi}{3}) cm). Tính quãng đường vật đi được trong khoảng thời gian từ 1,5s đến 3s là:
- Vật dao động điều hòa theo phương trình (x = 10 cos(pi t - frac{pi }{ 2}) cm.Tính quãng đường vật đi được trong khoảng thời gian từ 1,5s đến 13/3s là:
- Một vật dao động điều hòa với phương trình (x = 4sqrt{2}cos(5 pi t - frac{pi}{4})) cm. Quãng đường vật đi được từ thời điểm t1 = 0,1 s đến t2 = 6s
- Một vật dao động điều hòa với phương trình (x = 5 cos(4 pi t + pi/3))cm. Xác định quãng đường vật đi được sau 7T/12 s
- Vật dao động điều hòa với phương trình (x = A cos (6 pi t + frac{pi}{3})) sau (frac{7T}{12}) vật đi được quãng đường 10cm.
- Một vật dao động điều hòa với phương trình (x = A cos(6 pi t + pi / 4)) cm.Sau T/4 kể từ thời điểm ban đầu vật đi được quãng đường là 10 cm
- Vật dao động điều hòa với phương trình (x = A cos (8 pi t + frac{pi}{4})).Tìm quãng đường vật đi được sau khoảng thời gian T/8 kể từ thời điểm ban đầu?






