-
Câu hỏi:
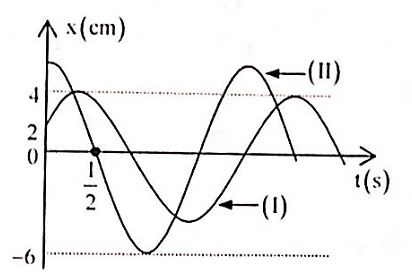
Hai dao động điều hòa cùng phương theo phương trình: \({x_1} = {A_1}\cos \left( {\omega t + {\varphi _1}} \right)cm;{x_2} = {A_2}\cos \left( {\omega t + {\varphi _2}} \right)\) (cm) trên hình vẽ đường đồ thị (I) biểu diễn dao động thứ nhất, đường đồ thị (II) biểu diễn dao động tổng hợp của hai dao động. Phương trình vận tốc của dao động thứ hai là:
- A. \({v_2} = 2\sqrt 7 \cos \left( {\pi t + 0,714} \right)\)cm/s
- B. \({v_2} = 2\pi \sqrt 3 \cos \left( {\pi t + 2,285} \right)\)cm/s
- C. \({v_2} = 2\pi \sqrt 7 \cos \left( {\pi t + 2,285} \right)\)cm/s
- D. \({v_2} = 4\pi \sqrt 3 \cos \left( {2\pi t + 2,285} \right)\)cm/s
Lời giải tham khảo:
Đáp án đúng: C
+ Lúc t = 0 dao động II ở biên, đến thời điểm t = 0,5 s thì dao động II ở VTCB nên:
\(\frac{T}{4} = 0,5 \Rightarrow T = 2\left( s \right) \Rightarrow \omega = \pi \) (rad/s)
+ Lúc t = 0, dao động II đang ở biên nên phương trình dao động tổng hợp là:
x = 6cos πt (cm)
+ Lúc t = 0, vật I đang ở \(\left\{ \begin{array}{l}
{x_1} = 2\left( {cm} \right) = \frac{A}{2}\\
{v_1} > 0
\end{array} \right.\) nên phương trình dao động 1 là:\({x_1} = 4\cos \left( {\pi t - \frac{\pi }{3}} \right)\) (cm)
+ Phương trình dao động thứ 2 là:
\(\begin{array}{l}
x = {x_1} + {x_2}\\
\Rightarrow {x_2} = x - {x_1} = 6\cos \pi t - 4\cos \left( {\pi t - \frac{\pi }{3}} \right) = 2\sqrt 7 \cos \left( {\pi t + 0,714} \right)\\
\Rightarrow {v_2} = {\left( {{x_2}} \right)^/} = 2\pi \sqrt 7 \cos \left( {\pi t + 0,714 + \frac{\pi }{2}} \right)
\end{array}\)
Câu hỏi này thuộc đề thi trắc nghiệm dưới đây, bấm vào Bắt đầu thi để làm toàn bài
Hướng dẫn Trắc nghiệm Online và Tích lũy điểm thưởng
CÂU HỎI KHÁC
- Trong sự truyền sóng cơ, để phân loại sóng ngang và sóng dọc căn cứ vào:
- Phương trình x=10cos(ωt+φ)cm của vật dao động điều hòa tại thời điểm t
- Một con lắc đơn có độ dài l thì dao động điều hòa với chu kì T
- Cho mạch RLC nối tiếp có \({U_L}\; = {\rm{ }}{U_R}\; = {\rm{ }}0,5{U_C}\)
- Một chất điểm dddh có tốc độ khi qua vị trí cân bằng là 8π cm/s
- Câu nào đúng. Tia α
- Một nguồn sáng có công suất 10mW phát ra bức xạ đơn sắc có bước sóng λ
- Phát biểu nào về ánh sáng sau đây đúng?
- Công thoát electron của KL làm catôt của một tế bào quang điện là 4,5eV
- Đối với một chất phỏng xạ, sự phóng xạ xảy ra
- Pin quang điện biến đổi trực tiếp
- Khi nói về tia tử ngoại, nhận định nào dưới đây là sai?
- Đoạn mạch điện xoay chiều khi gồm hai phần tử R và C mắc nối tiếp.
- Chiết suất của một môi trường có giá trị
- Một CLLX nằm ngang dao động điều hòa với phương trình:
- Tia X không có tính chất nào sau đây
- Khoảng cách giữa hai điểm trên phương truyền sóng gần nhau nhất
- Nguyên tắc hoạt động của 1 máy quang phổ dựa trên hiện tượng
- 1 mạch RLC, cuộn dây thuần cảm mắc vào mạng điện sinh hoạt 220 V-50 Hz.
- Khi truyền âm từ không khí vào trong nước, kết luận nào không đúng?
- Hệ thức đúng trong một mạch dao động LC lí tưởng gồm cuộn cảm thuần L
- Khi nói về sóng điện từ, điều nào sau đây là sai?
- Trong thí nghiệm Y-âng, hai khe chiếu ánh sáng đơn sắc có bước sóng λ.
- Tại mặt chất lỏng nằm ngang có hai nguồn sóng O1, O2 cách nhau 24 cm
- Nguồn âm điểm O phát sóng âm đẳng hướng ra môi trường không hấp thụ
- 1 sóng dừng trên sợi dây đàn hồi dài với bước sóng 60 cm.
- Tự cảm 20 μΗ và một tụ xoay có điện dung (là hàm bậc nhất của góc xoay)
- Trong thí nghiệm Y-âng về giao thoa ánh sáng đơn sắc có bước sóng λ
- Nguyên tử hidro ở trạng thái cơ bản có bán kính r0
- Hạt α có động năng 5,3 MeV bắn vào hạt nhân Be9 đứng yên
- Năng lượng liên kết là NL tỏa ra khi tạo thành nguyên tử từ các nuclon
- Một bệnh nhân điều trị bằng đồng vị phóng xạ, dùng tia γ diệt tế bào bệnh
- Đoạn mạch AB gồm cuộn cảm thuần nối tiếp với tụ điện
- Một con lắc đơn có khối lượng m = 0,5 kg, chiều dài l = 0,5m
- Đặt điện áp u = U√2cos(ωt), (U, ω không đổi) vào hai đầu đoạn mạch R,L,C
- Hai dao động điều hòa cùng phương theo phương trình:
- Có ba máy biến áp lý tưởng cuộn thứ cấp của các máy có số vòng bằng nhau
- Một chất điểm dao động với phương trình x = 10cos2πt (cm).
- Mạch xoay chiều AB gồm điện trở thuần R, cuộn cảm thuần có độ tự cảm L
- Lần lượt đặt vào 2 đầu đoạn mạch RLC nối tiếp (R là biến trở,L thuần cảm)







