-
Câu hỏi:
Đặt điện áp \(u = 50\cos \left( {\omega t + \varphi } \right)\) (ω không đổi và \(\frac{\pi }{4} < \varphi < \frac{\pi }{2}\) vào hai đầu đoạn mạch mắc nối tiếp theo thứ tự: điện trở R, cuộn cảm thuần L với ZL = √3.R và tụ điện có điện dung C thay đổi được. Khi C = C1 thì điện áp hiệu dụng giữa hai đầu tụ điện là cực đại và V. Khi C = C2 thì điện áp giữa hai đầu đoạn mạch chữa R và L là V. Giá trị của U0 gần nhất giá trị nào sau đây?
- A. 87 V
- B. 60 V
- C. 77 V
- D. 26 V
Lời giải tham khảo:
Đáp án đúng: A
Ta có:
- R, L không đổi → φRL là hằng số → ∆φRL_C cũng là hằng số.
- \(\overrightarrow {{U_{AB}}} = \overrightarrow {{U_{RL}}} + \overrightarrow {{U_C}} \)→ M có quỹ tích là đường tròn.
- \({\varphi _{RL}} = arctan\left( {\frac{{{Z_L}}}{R}} \right) = arctan\left( {\sqrt 3 } \right) = {60^0}\)→ \(\alpha = {30^0}\).
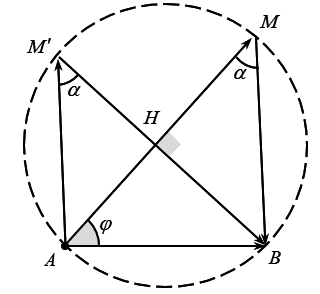
Từ giản đồ vecto
- C = C1 thì UCmax → AM là đường kính của đường tròn và góc ABM là góc vuông.
\(\varphi = arc\cos \left( {\frac{{AB}}{{AM}}} \right) = arc\cos \left( {\frac{{50}}{{100}}} \right) = {60^0}\)
→ \(HB = AB\sin \varphi = \left( {50} \right)\sin \left( {60} \right) = 25\sqrt 3 \)V và \(AH = AB\cos \varphi = \left( {50} \right)\cos \left( {{{60}^0}} \right) = 25\)V.
- ∆AM’H vuông tại H → \(M'H = \frac{{AH}}{{\tan \alpha }} = \frac{{\left( {25} \right)}}{{\tan \left( {{{30}^0}} \right)}} = 25\sqrt 3 \)V.
→ \({U_0} = HB + AM' = \left( {25\sqrt 3 } \right) + \left( {25\sqrt 3 } \right) \approx 87\)V.
Câu hỏi này thuộc đề thi trắc nghiệm dưới đây, bấm vào Bắt đầu thi để làm toàn bài
Hướng dẫn Trắc nghiệm Online và Tích lũy điểm thưởng
CÂU HỎI KHÁC
- Đặt hiệu điện thế U vào hai đầu một đoạn mạch điện
- Một mạch kín phẳng, hình vuông cạnh a
- Mối liên hệ giữa tần số góc ω và chu kì T
- Chọn phát biểu sai. Một con lắc lò xo
- Một vật dao động tắt dần thì các đại lượng giảm dần
- Công thức liên hệ giữa bước sóng λ
- Trong giao thoa sóng cơ, để hai sóng có thể giao thoa
- Tốc độ truyền âm có giá trị lớn nhất
- Cường độ dòng điện i = 4 cos (120πt) A
- Đặt điện áp xoay chiều có tần số góc ω
- Khi hoạt động, máy phát điện xoay chiều ba pha
- Một máy hạ áp lí tưởng có số vòng dây của cuộn sơ cấp
- Mạch dao động lí tưởng gồm tụ điện có điện dung C
- Trong chân không, sóng điện từ có bước sóng
- Màu sắc sặc sỡ trên các bong bóng xà phòng
- Tia X với tia nào sau đây có cùng bản chất
- Theo thuyết lượng tử ánh sáng, ánh sáng được tạo thành bởi các hạt nào
- Xét nguyên tử hidro theo mẫu nguyên tử Bo. Biết r0 là bán kính Bo.
- Số proton có trong hạt nhân
- Tia ß+ là dòng các
- Một điện tích điểm q
- Một con lắc đơn có chiều dài 0,5 m
- Trên một sợi dây đàn hồi có một đầu cố định
- Đặt điện áp xoay chiều có giá trị hiệu dụng U
- Đặt điện áp xoay chiều vào hai đầu điện trở R
- Một sóng điện từ có tần số
- Trong thí nghiệm Y – âng về giao thoa ánh sáng, khoảng vân trên màn quan sát là
- Trong chân không, bức xạ có bước sóng nào
- Khi chiếu bức xạ đơn sắc mà photon của nó có năng lượng ε
- Hạt nhân He có độ hút khối
- Tác dụng vào hệ dao động một ngoại lực
- Một người có mặt không bị tật và có khoảng cực cận là 25 cm
- Dao động của một vật là tổng hợp của hai dao động
- Chất điểm A chuyển động tròn đều trên đường tròn bán kính R
- Một sợi dây đàn hồi căng ngang với hai đầu cố định
- Trong giờ thực hành đo độ tự cảm của một cuộn dây
- Một con lắc lò xo gồm một vật nhỏ khối lượng m
- Ở mặt chất lỏng, tại hai điểm S1 và S2
- Đặt điện áp (ω không đổi)
- Điện năng được truyền từ một nhà máy phát điện gồm 8 tổ máy