Cho hai khẳng định sau:(I) Nếu một hình nào đó có hai trục đối xứng vuông góc với nhau thì hình đó có tâm đối xứ

Xét khẳng định (I).

Gọi O là giao điểm của hai trục đối xứng a và b hình (H).

Với điểm M bất kì thuộc (H), ta có:

Đ_a(M)=M₁ suy ra OM=OM₁ và \(\widehat {{O_1}} = \widehat {{O_2}}\)

Đ_b(M)=M₁ suy ra OM₁=OM₂ và \(\widehat {{O_3}} = \widehat {{O_4}.}\)

Do đó: \(\left\{ \begin{array}{l}OM = O{M_2}\\\widehat {MO{M_2}} = {180^0}\end{array} \right. \Rightarrow \) Đ_o(M)=M₂.

Vây (I) đúng.

Xét khẳng định (II):

Có thể thực hiện được, cụ thể:

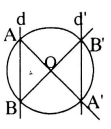
+ Lấy điểm A trên d, dùng thước thẳng dựng tia AO.

+ Dùng compa dựng đường tròn (O;OA), đường tròn này cắt đường thẳng d tại B và tia OA tại A’.

+ Dùng thước thẳng dựng tia BO cắt đường tròn tại B’.

+ Dùng thước thẳng nối A’ và B’ ta được đường thẳng d’ cần dựng.