1. Hiện tượng nhiễu xạ ánh sáng.

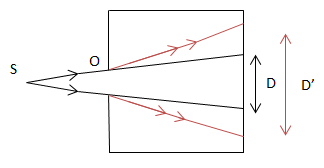
KL: Khi ánh sáng truyền qua lỗ tròn nhỏ (khe hẹp) thì không liên thông theo đinh luật truyền thẳng ⇒ Ánh sáng gây ra hiện tượng nhiễu xạ.
2. Hiện tượng giao thoa ánh sáng
* Thí nghiệm Yâng (Thomas Young)

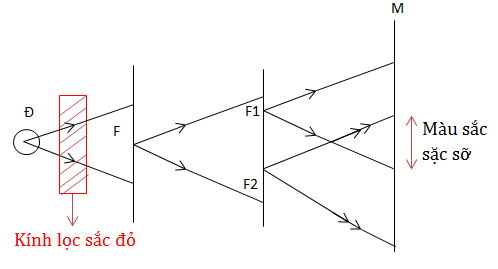
Kết luận: Khi chiếu ánh sáng đơn sắc \(\lambda\) thì trên màn thu được hệ thống các vân sáng và vân tối xen kẻ 1 cách liên tục.
⇒ Ánh sáng có bản chất là sóng.
* Vị trí các vân giao thoa

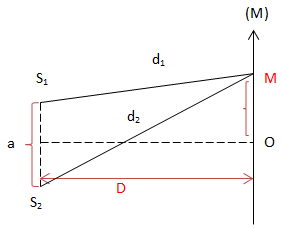
Với a = S₁S₂; D khoảng cách từ mặt phẳng chứa S₁S₂ → Màu d₁d₂ là khoảng cách từ M đến S₁S2
\(\lambda\): là bước sóng của ánh sáng đơn sắc.
\(\Rightarrow d_2-d_1=\frac{a.x}{D}\)
* Vị trí vân sáng (cực đại): \(d_2-d_1=k.\lambda\)
 \(\Rightarrow \frac{a.x_s}{D}=k.\lambda \Rightarrow x_s=k.\frac{\lambda .D}{a}, k=0,\pm 1,\pm 2\)
* Vị trí các vân tối (cực tiểu): \(d_2-d_1= (k'+\frac{1}{2}).\lambda\)
\(\Rightarrow \frac{a.x_t}{D}=(k'+\frac{1}{2})\lambda \Rightarrow x_t=(k'+\frac{1}{2} ).\frac{\lambda .D}{a}, k'\in Z\)
* Khoảng vân (i): là khoảng cách giữa 2 vân sáng hoặc 2 vân tối kề nhau
\(i=\frac{\lambda .D}{a}\)
+ \(x_s=k.i\)
+ \(x_t=(k'+\frac{1}{2})i\)
* Ứng dụng: Đo \(\lambda\) của ánh sáng 
Từ \(i=\frac{\lambda .D}{a}\Rightarrow \lambda =\frac{a.i}{D}\)
3. Bước sóng và màu sắc ánh sáng (SGK)