Ở lớp 10, khi học về chuyển động của vật, ta đã biết có sự chuyển hóa giữa động năng và thế năng của vật. Vậy trong dao động điều hòa có sự chuyển hóa tương tự không? Hãy cùng HOC247 tìm hiểu qua nội dung của Bài 5: Động năng. Thế năng. Sự chuyển hóa năng lượng trong dao động điều hòa trong chương trình Vật lí 11 Kết nối tri thức. Mời các em cùng tham khảo!
Tóm tắt lý thuyết
1.1. Động năng
- Động năng của vật dao động điều hòa được xác định bởi biểu thức
\({{\rm{W}}_d} = \frac{1}{2}m{\omega ^2}({A^2} - {x^2})\)
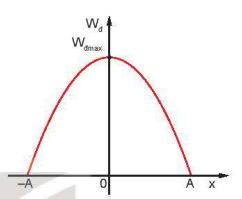
Hình 5.1. Sự biến thiên của động năng Wđ theo li độ x
- Đồ thị cho thấy, khi vật đi từ VTCB tới vị trí biên thì động năn của vật đang từ cực đại giảm đến 0. Khi vật đi từ vị trí biên về VTCB thì động năng của vật tăng từ 0 đến giá trị cực đại.
1.2. Thế năng
- Theo định luật bảo toàn năng lượng, nếu bỏ qua ma sát thì động năng của vật không mất đi mà chuyển dần thành thế năng của vật và ngược lại nên ta có:
\({{\rm{W}}_t} = \frac{1}{2}m{\omega ^2}{x^2}\)
Hình 5.2. Sự biến thiên của động năng Wt theo li độ x
- Đồ thị biến thiên thế năng theo li độ x cũng là một đường Parabol nhưng bề lõm hướng lên như hình 5.2 và có giá trị cực đại:
\({{\rm{W}}_{t\max }}{\rm{ = }}{{\rm{W}}_{d\max }} = \frac{1}{2}m{\omega ^2}{A^2}\)
1.3. Cơ năng
Trong dao động điều hòa, có sự chuyển hóa qua qua lại giữa động năng và thế năng của vật, còn cơ năng, tức tổng động năng và thế năng thì được bảo toàn
\(W = {{\rm{W}}_d} + {{\rm{W}}_t} = \frac{1}{2}m{\omega ^2}{A^2}\)
1.4. Cơ năng của con lắc đơn và con lắc lò xo
1.4.1. Con lắc lò xo
Hình 5.3. Con lắc lò xo
- Nếu bỏ qua ma sát thì dao động của con lắc lò xo là dao động điều hòa
- Chọn mốc thế năng ở VTCB thì thế năng của con lắc lò xo khi ở li độ x là:
\({{\rm{W}}_t} = \frac{1}{2}k{x^2}\)
Với k là độ cứng lò xo
Ta có: \(\omega = \sqrt {\frac{k}{m}} \) và chu kì của con lắc lò xo là: \(T = 2\pi \sqrt {\frac{m}{k}} \)
- Cơ năng của con lắc lò xo: \(W = {{\rm{W}}_d} + {{\rm{W}}_t} = \frac{1}{2}m{\omega ^2}{A^2}\) = hằng số.
1.4.2. Con lắc đơn
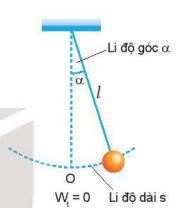
- Vị trí của con lắc đơn được xác định bằng li độ dài s hay li độ góc \(\alpha \)
Hình 5.4. Con lắc đơn
- Thế năng của con lắc đơn là thế năng trọng trường. Chọn mốc thế năng ở VTCB thì thế năng của con lắc ở li độ góc \(\alpha \) là:
\({{\rm{W}}_t} = mgl\frac{{{\alpha ^2}}}{2} = \frac{1}{2}m\frac{g}{l}{s^2}\)
- Ta có: \(\omega = \sqrt {\frac{g}{l}} \)
- Tương tự với con lắc lò xo ta có: \(W = {{\rm{W}}_d} + {{\rm{W}}_t} = \frac{1}{2}m{\omega ^2}{A^2}\) = hằng số.
|
Một vật có khối lượng m dao động điều hòa với tần số góc \(\omega \) và biên độ A. Tại li độ x: - Động năng của vật là: \({{\rm{W}}_d} = \frac{1}{2}m{\omega ^2}({A^2} - {x^2})\) - Thế năng của con lắc là: \({{\rm{W}}_t} = \frac{1}{2}m{\omega ^2}{x^2}\) - Cơ năng của con lắc là: \(W = {{\rm{W}}_d} + {{\rm{W}}_t} = \frac{1}{2}m{\omega ^2}{A^2}\) = hằng số |
Bài tập minh họa
Bài tập 1: Một con lắc lò xo có khối lượng vật nhỏ là 50 g. Con lắc dao động điều hòa theo một trục cố định nằm ngang với phương trình \(x = A\cos \omega t\). Cứ sau những khoảng thời gian 0,05 s thì động năng và thế năng của vật lại bằng nhau. Lấy \({\pi ^2} = 10\). Tính độ cứng của con lắc lò xo?
Hướng dẫn giải:
Động năng của vật bằng thế năng sau các khoảng thời gian t = 0,25T
=> 0,5 = 0,25T => T = 0,2 s
-> Độ cứng của lò xo \(k = m{\omega ^2} = m{\left( {\frac{{2\pi }}{T}} \right)^2} = 50N/m\)
Bài tập 2: Một con lắc lò xo gồm vật nhỏ và con lắc có độ cứng 20 N/m dao động điều hòa với chu kì 2 s. Khi pha dao động là 0,5\(\pi \) thì vận tốc của vật là \( - 20\sqrt 3 \) cm/s. Lấy \({\pi ^2} = 10\). Tính động năng của con lắc khi vật đi qua vị trí có li độ 3\(\pi \) cm.
Hướng dẫn giải:
Khi dao động có pha là 0,5\(\pi \) → vật đi qua vị trí cân bằng theo chiều âm
\(v = - \omega A = - 20\sqrt 3 cm \to A = 2\sqrt 3 \pi cm\)
Động năng của con lắc tại vị trí x = 3\(\pi \) cm
\(\begin{array}{l}
{W_d} = {\rm{W - }}{{\rm{W}}_t} = \frac{1}{2}k({A^2} - {x^2})\\
= \frac{1}{2}.20\left[ {{{(2\sqrt 3 \pi )}^2} - {{\left( {3\pi } \right)}^2}} \right]{.10^{ - 4}} = 0,03J
\end{array}\)
Luyện tập Bài 5 Vật lý 11 Kết nối tri thức
Học xong bài này các em cần biết:
- Công thức tính động năng, thế năng, cơ năng
- Sự chuyển hóa giữa động năng và thế năng của vật dao động điều hòa
3.1. Trắc nghiệm Bài 5 Vật lý 11 Kết nối tri thức
Các em có thể hệ thống lại nội dung kiến thức đã học được thông qua bài kiểm tra Trắc nghiệm Vật lí 11 Kết Nối Tri Thức Bài 5 cực hay có đáp án và lời giải chi tiết.
-
- A. hợp lực tác dụng vào vật có giá trị lớn nhất khi vật đi qua vị trí cân bằng.
- B. động năng của vật biến đổi tuần hoàn với chu kì bằng một nửa chu kì dao động của vật.
- C. tốc độ của vật lớn nhất khi vật đi qua vị trí cân bằng.
- D. vận tốc của vật lệch pha 0,5m với li độ dao động.
-
- A. \(\frac{1}{4}m{\omega ^2}{A^2}\)
- B. \(m{\omega ^2}{A^2}\)
- C. \(\frac{1}{2}m{\omega ^2}{A^2}\)
- D. \(\frac{1}{3}m{\omega ^2}{A^2}\)
-
- A. \(m{\omega ^2}{x^2}\)
- B. \(\frac{1}{2}m{\omega ^2}{x^2}\)
- C. \({m^2}\omega x\)
- D. \(\frac{1}{2}{m^2}{\omega ^2}x\)
Câu 4-10: Mời các em đăng nhập xem tiếp nội dung và thi thử Online để củng cố kiến thức về bài học này nhé!
3.2. Bài tập SGK Bài 5 Vật lý 11 Kết nối tri thức
Các em có thể xem thêm phần hướng dẫn Giải bài tập Vật lí 11 Kết Nối Tri Thức Bài 5 để giúp các em nắm vững bài học và các phương pháp giải bài tập.
Khởi động trang 20 SGK Vật lí 11 Kết nối tri thức – KNTT
Hoạt động trang 21 SGK Vật lí 11 Kết nối tri thức – KNTT
Hoạt động 1 trang 22 SGK Vật lí 11 Kết nối tri thức – KNTT
Giải Câu hỏi trang 22 SGK Vật lí 11 Kết nối tri thức – KNTT
Hoạt động 2 trang 22 SGK Vật lí 11 Kết nối tri thức – KNTT
Giải Câu hỏi trang 23 SGK Vật lí Kết nối tri thức - KNTT
Hỏi đáp Bài 5 Vật lý 11 Kết nối tri thức
Trong quá trình học tập nếu có thắc mắc hay cần trợ giúp gì thì các em hãy comment ở mục Hỏi đáp, Cộng đồng Vật lý HOC247 sẽ hỗ trợ cho các em một cách nhanh chóng!
Chúc các em học tập tốt và luôn đạt thành tích cao trong học tập!
-- Mod Vật Lý 11 HỌC247