Nhằm giúp các em có thể tìm được cách phân tích các lực một cách dễ dàng HOC247 xin giới thiệu nội dung Bài 13: Tổng hợp lực – Phân tích lực trong Chương 5 Vật Lý 10 Chân trời sáng tạo. Mời các em cùng tham khảo!
Tóm tắt lý thuyết
1.1. Tổng hợp và phân tích lực
a. Phương pháp tổng hợp lực trên một mặt phẳng
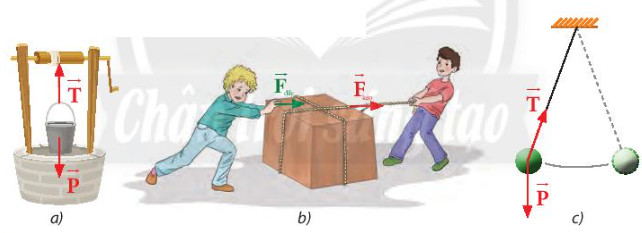
Lực tác dụng lên một số vật trong thực tiễn:
a) gàu nước đang được kéo lên
b) thùng hàng đang dịch chuyển về bên phải
c) con lắc đang chuyển động
|
Lực tổng hợp là một lực thay thế các lực tác dụng đồng thời vào cùng một vật, có tác dụng giống hệt các lực ấy. |
|---|
- Quy tắc hình bình hành: Lực tổng hợp \(\overrightarrow {{F_t}} = \overrightarrow {{F_1}} + \overrightarrow {{F_2}} \) của hai lực đồng quy \(\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} \) được biểu diễn bởi vecto đường chéo của hình bình hành. Khi này, gốc hai vecto lực phải trùng nhau.
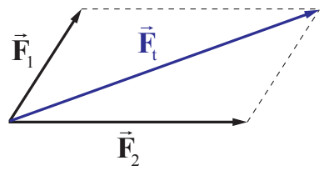
- Quy tắc tam giác lực: Ta có thể tịnh tiến vecto lực \(\overrightarrow {{F_2}} \) sao cho gốc của nó trùng với ngọn của vecto \(\overrightarrow {{F_1}} \). Khi này, vecto lực tổng hợp \(\overrightarrow {{F_t}} \) là vecto nối gốc của \(\overrightarrow {{F_1}} \) với ngọn của \(\overrightarrow {{F_2}} \).

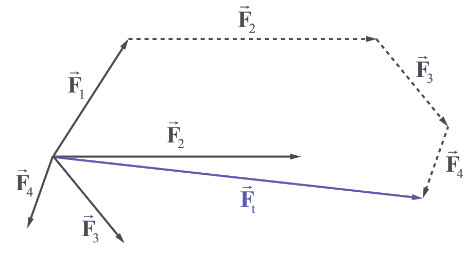
- Khi vật chịu tác dụng của nhiều hơn hai lực. Ta có thể áp dụng một cách liên tiếp quy tắc tam giác lực để tìm hợp lực. Quy tắc này gọi là quy tắc đa giác lực
 |
 |
| Lực T là lực tổng hợp của các lực thành phần T1 và T2 | |
b. Phương pháp phân tích một lực thành các lực thành phần vuông góc
- Trong nhiều trường hợp, ta cần phân tích một lực thành hai thành phần vuông góc với nhau để có thể giải quyết bài toán cụ thể.
- Cần phải xác định được các phương tác dụng của lực để phân tích.
- Ví dụ:
+ Khối gỗ được kéo trượt trên mặt phẳng ngang
.jpg) |
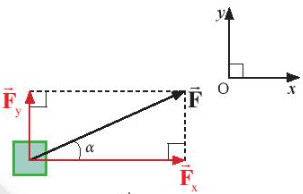 |
| Lực kéo | Phân tích lực kéo |
+ Người chơi trượt cát từ đỉnh đồi theo một mặt phẳng nghiêng
 |
 |
| Lực đẩy | Phân tích trọng lực P |
1.2. Thí nghiệm tổng hợp lực
a. Thí nghiệm 1: Tổng hợp hai lực đồng quy
- Thí nghiệm:
+ Bước 1: Bố trí thí nghiệm theo gợi ý ở Hình dưới đây:
. Hiệu chỉnh lực kế (điều chỉnh lực kế sao cho khi chưa đo lực thì kim chỉ thị nằm đúng vạch số 0).
. Móc một đầu lò xo vào chốt của đế nam châm gắn trên bảng từ.
. Móc hai lực kế gắn lên bảng vào đầu đưới của lò xo nhờ sợi đây ba nhánh.
+ Bước 2: Kéo hai lực kế về hai phía cho lò xo đãn ra một đoạn (trong giới hạn đàn hồi).

Gợi ý bố trí thí nghiệm
+ Bước 3: Đặt thước do góc lên bảng từ sao cho tâm thước trùng với vị trí giao nhau của ba nhánh dây. Lưu ý dùng êke ba chiều để căn chỉnh dây nối lò xo có phương trùng với vạch số 0.
+ Bước 4: Đo góc \(\alpha \) hợp bởi hai nhánh dây nối với lực kế, đọc số chỉ số đo của hai lực kế F1, F2
- Lực tổng hợp \(\overrightarrow {{F_t}} \) nằm trên đường chéo của hình bình hành với 2 cạnh là 2 lực thành phần \(\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} \)
b. Thí nghiệm 2: Tổng hợp hai lực song song cùng chiều
* Thí nghiệm:
- Bước 1: Bố trí thí nghiệm theo gợi ý: gắn hai đầu thước nhôm nhẹ với hai lò xo và treo lên bảng từ bằng hai nam châm.
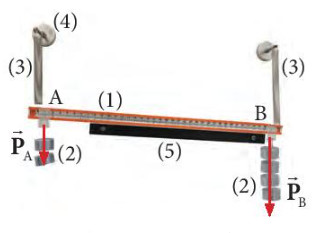
- Bước 2: Treo vào hai điểm A, B ở hai đầu của thước nhôm một số quả cân (khối lượng mỗi bên khác nhau). Đánh dấu vị trí cân bằng mới này của thước nhờ vào êke ba chiểu (Hình 13.12). Ghi giá trị trọng lượng PA, PB của các quả cân mỗi bên.
- Bước 3: Treo các quả cân vào cùng một vị trí trên thước AB (số lượng các quả cân và vị trí treo có thể thay đổi) sao cho thước trở lại đúng vị trí đánh dấu lúc đầu (Hình 13.13). Đo các giá trị AO và BO trên thước
Lưu ý: Thực hiện thí nghiệm 3 lần và ghi số liệu vào bảng
 |
 |
|
Hình 13.12. Gợi ý bố trí thí nghiệm để tổng hợp hai lực song song |
Hình 13.13. Treo các quả cân sao cho lục cân bằng như trước |
- Từ kết quả ta thấy:
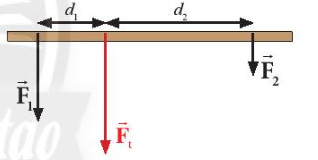
Minh họa tổng hợp hai lực song song cùng chiều
|
Lực tổng hợp của hai lực song song cùng chiều là một lực: + Song song, cùng chiều với các lực thành phần + Có độ lớn bằng tổng độ lớn của các lực: \({F_t} = {F_1} + {F_2}\) + Có giá nằm trong mặt phẳng của hai lực thành phần, chia khoảng cách giữa hai giá của hai lực song song thành những đoạn tỉ lệ nghịch với độ lớn của hai lực ấy: \(\frac{{{F_1}}}{{{F_2}}} = \frac{{{d_2}}}{{{d_1}}}\) |
|---|
Bài tập minh họa
Bài tập 1: Độ lớn của hợp lực hai lực đồng quy hợp với nhau góc \(\alpha \) thỏa mãn biểu thức nào?
Hướng dẫn giải:
Áp dụng quy tắc hình bình hành ta có độ lớn của hợp lực là \(F = \sqrt {F_1^2 + F_2^2 + 2.{F_1}.{F_2}.c{\rm{os}}\alpha } \)
Bài tập 2: Cho hai lực đồng quy có cùng độ lớn 600 N. Hỏi góc giữa 2 lực bằng bao nhiêu thì hợp lực cũng có độ lớn bằng 600 N?
Hướng dẫn giải:
Áp dụng quy tắc hình bình hành ta có:
\(\begin{array}{l}
{F^2} = F_1^2 + F_2^2 + 2.{F_1}.{F_2}.c{\rm{os}}\alpha \\
\Rightarrow {\rm{60}}{{\rm{0}}^2} = {600^2} + {600^2} + 2.600.600.c{\rm{os}}\alpha \\
\Rightarrow \alpha = {120^0}
\end{array}\)
Bài tập 3: Ba lực có cùng độ lớn bằng 10 N trong đó \({\vec F_1}\) và \({\vec F_2}\) hợp với nhau góc 600. Lực \({\vec F_3}\) vuông góc mặt phẳng chứa \({\vec F_1}\) và \({\vec F_2}\). Hợp lực của ba lực này có độ lớn bao nhiêu?
Hướng dẫn giải:
- Độ lớn hợp lực của hai lực \({\vec F_1}\) và \({\vec F_2}\) là \({F_{1,2}} = 2.{F_1}.c{\rm{os}}\frac{\alpha }{2} = 2.10.c{\rm{os}}{30^0} = 10\sqrt 3 N\)
- Lực \({\vec F_3}\) vuông góc mặt phẳng chứa \({\vec F_1}\) và \({\vec F_2}\) nên \({\vec F_3}\) vuông góc với \({\vec F_{1,2}}\) suy ra độ lớn của hợp lực là: \(F = \sqrt {F_3^2 + F_{1,2}^2} = \sqrt {{{\left( {10} \right)}^2} + {{\left( {10\sqrt 3 } \right)}^2}} = 20N\)
Luyện tập Bài 13 Vật Lý 10 CTST
Sau bài học này, học sinh sẽ nắm được:
- Tổng hợp lực, phân tích lực
- Thiết kế và thực tiễn thí nghiệm tổng hợp hai lực đồng quy, song song
3.1. Trắc nghiệm Bài 13 môn Vật Lý 10 CTST
Các em có thể hệ thống lại nội dung kiến thức đã học được thông qua bài kiểm tra Trắc nghiệm Vật Lý 10 Chân trời sáng tạo Chương 5 Bài 13 cực hay có đáp án và lời giải chi tiết.
Câu 4-10: Mời các em đăng nhập xem tiếp nội dung và thi thử Online để củng cố kiến thức về bài học này nhé!
3.2. Bài tập SGK Bài 13 môn Vật Lý 10 CTST
Các em có thể xem thêm phần hướng dẫn Giải bài tập Vật Lý 10 Chân trời sáng tạo Chương 5 Bài 13 để giúp các em nắm vững bài học và các phương pháp giải bài tập.
Mở đầu trang 80 SGK Vật Lý 10 Chân trời sáng tạo - CTST
Câu hỏi thảo luận 1 trang 80 SGK Vật Lý 10 Chân trời sáng tạo - CTST
Câu hỏi thảo luận 2 trang 81 SGK Vật Lý 10 Chân trời sáng tạo - CTST
Luyện tập trang 81 SGK Vật Lý 10 Chân trời sáng tạo - CTST
Câu hỏi thảo luận 3 trang 82 SGK Vật Lý 10 Chân trời sáng tạo - CTST
Luyện tập trang 82 SGK Vật Lý 10 Chân trời sáng tạo - CTST
Vận dụng trang 83 SGK Vật Lý 10 Chân trời sáng tạo - CTST
Câu hỏi thảo luận 4 trang 83 SGK Vật Lý 10 Chân trời sáng tạo - CTST
Câu hỏi thảo luận 5 trang 83 SGK Vật Lý 10 Chân trời sáng tạo - CTST
Câu hỏi thảo luận 6 trang 84 SGK Vật Lý 10 Chân trời sáng tạo - CTST
Câu hỏi thảo luận 7 trang 85 SGK Vật Lý 10 Chân trời sáng tạo - CTST
Luyện tập trang 85 SGK Vật Lý 10 Chân trời sáng tạo - CTST
Vận dụng trang 86 SGK Vật Lý 10 Chân trời sáng tạo - CTST
Giải bài tập 1 trang 86 SGK Vật Lý 10 Chân trời sáng tạo - CTST
Giải bài tập 2 trang 86 SGK Vật Lý 10 Chân trời sáng tạo - CTST
Giải bài tập 3 trang 86 SGK Vật Lý 10 Chân trời sáng tạo - CTST
Giải bài tập trắc nghiệm 13.1 trang 40 SBT Vật lý 10 Chân trời sáng tạo - CTST
Giải bài tập trắc nghiệm 13.2 trang 40 SBT Vật lý 10 Chân trời sáng tạo - CTST
Giải bài tập trắc nghiệm 13.3 trang 41 SBT Vật lý 10 Chân trời sáng tạo - CTST
Giải bài tập trắc nghiệm 13.4 trang 41 SBT Vật lý 10 Chân trời sáng tạo - CTST
Giải bài tập tự luận 13.1 trang 41 SBT Vật lý 10 Chân trời sáng tạo - CTST
Giải bài tập tự luận 13.2 trang 41 SBT Vật lý 10 Chân trời sáng tạo - CTST
Giải bài tập tự luận 13.3 trang 42 SBT Vật lý 10 Chân trời sáng tạo - CTST
Giải bài tập tự luận 13.4 trang 42 SBT Vật lý 10 Chân trời sáng tạo - CTST
Giải bài tập tự luận 13.5 trang 42 SBT Vật lý 10 Chân trời sáng tạo - CTST
Hỏi đáp Bài 13 Vật Lý 10 CTST
Trong quá trình học tập nếu có thắc mắc hay cần trợ giúp gì thì các em hãy comment ở mục Hỏi đáp, Cộng đồng Vật lý HOC247 sẽ hỗ trợ cho các em một cách nhanh chóng!
Chúc các em học tập tốt và luôn đạt thành tích cao trong học tập!
-- Mod Vật Lý 10 HỌC247







