DŲ░ß╗øi ─æ├óy l├Ā HŲ░ß╗øng dß║½n giß║Żi b├Āi tß║Łp H├¼nh hß╗Źc 11 n├óng cao ChŲ░ŲĪng 3 B├Āi 5 Khoß║Żng c├Īch ─æŲ░ß╗Żc hoc247 bi├¬n soß║Īn v├Ā tß╗Ģng hß╗Żp, nß╗Öi dung b├Īm s├Īt theo chŲ░ŲĪng tr├¼nh SGK To├Īn 11 n├óng cao gi├║p c├Īc em hß╗Źc sinh nß║»m vß╗»ng phŲ░ŲĪng ph├Īp giß║Żi b├Āi tß║Łp v├Ā ├┤n tß║Łp kiß║┐n thß╗®c hiß╗ću quß║Ż hŲĪn.
B├Āi 29 trang 117 SGK H├¼nh hß╗Źc 11 n├óng cao
Cho tß╗® diß╗ćn ABCD c├│ AC = BC = AD = BD = a, AB = c, CD = cŌĆÖ. T├Łnh khoß║Żng c├Īch giß╗»a hai ─æŲ░ß╗Øng thß║│ng AB v├Ā CD.
HŲ░ß╗øng dß║½n giß║Żi:
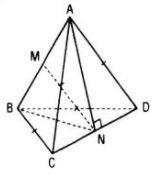
Gß╗Źi M, N lß║¦n lŲ░ß╗Żt l├Ā trung ─æiß╗ām cß╗¦a AB v├Ā CD
╬öACD c├ón n├¬n AN ŌŖź CD v├Ā ╬öBCD c├ón n├¬n BN ŌŖź CD.
Do ─æ├│ CD ŌŖź (ABN) suy ra CD ŌŖź MN.
TŲ░ŲĪng tß╗▒ ta c┼®ng c├│ AB ŌŖź MN
Vß║Ły d(AB, CD) = MN
Ta c├│:
\(\begin{array}{l}
M{N^2} = A{N^2} - A{M^2} = A{D^2} - N{D^2} - A{M^2}\\
= {a^2} - \frac{{c{\prime ^2}}}{4} - \frac{{{c^2}}}{4} = \frac{1}{4}(4{a^2} - c{\prime ^2} - {c^2})
\end{array}\)
Vß║Ły \(MN = \frac{1}{2}\sqrt {4{a^2} - c{\prime ^2} - {c^2}} \) vß╗øi ─æiß╗üu kiß╗ćn \(4{a^2} > {c^2} + c{\prime ^2}\)
B├Āi 30 trang 117 SGK H├¼nh hß╗Źc 11 n├óng cao
Cho h├¼nh l─āng trß╗ź ABC.AŌĆÖBŌĆÖCŌĆÖ c├│ tß║źt cß║Ż c├Īc cß║Īnh ─æß╗üu bß║▒ng a. G├│c tß║Īo bß╗¤i cß║Īnh b├¬n v├Ā mß║Ęt ─æ├Īy bß║▒ng 30╦Ü. H├¼nh chiß║┐u H cß╗¦a ─æiß╗ām A tr├¬n mß║Ęt phß║│ng (AŌĆÖBŌĆÖCŌĆÖ) thuß╗Öc ─æŲ░ß╗Øng thß║│ng BŌĆÖCŌĆÖ.
a. T├Łnh khoß║Żng c├Īch giß╗»a hai mß║Ęt phß║│ng ─æ├Īy
b. Chß╗®ng minh rß║▒ng hai ─æŲ░ß╗Øng thß║│ng AAŌĆÖ v├Ā BŌĆÖCŌĆÖ vu├┤ng g├│c, t├Łnh khoß║Żng c├Īch giß╗»a ch├║ng.
HŲ░ß╗øng dß║½n giß║Żi:
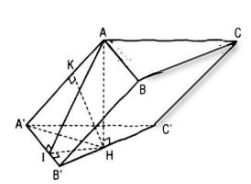
Ta c├│: AH ŌŖź (AŌĆÖBŌĆÖCŌĆÖ) n├¬n \(\widehat {AA'H}\) l├Ā g├│c giß╗»a AAŌĆÖ v├Ā mp(AŌĆÖBŌĆÖCŌĆÖ) do ─æ├│ \(\widehat {AA'H}\) = 300
Câu a:
Khoß║Żng c├Īch giß╗»a hai mp ─æ├Īy ch├Łnh l├Ā AH, ta c├│: \(AH = AA\prime sin{30^0} = \frac{a}{2}\)
Câu b:
Tam gi├Īc AHAŌĆÖ vu├┤ng tß║Īi H n├¬n \(A\prime H = AA\prime cos{30^0} = \frac{{a\sqrt 3 }}{2}\). V├¼ AŌĆÖBŌĆÖCŌĆÖ l├Ā tam gi├Īc ─æß╗üu cß║Īnh a, H thuß╗Öc ─æŲ░ß╗Øng thß║│ng BŌĆÖCŌĆÖ m├Ā \(A\prime H = \frac{{a\sqrt 3 }}{2}\) n├¬n AŌĆÖH ŌŖź BŌĆÖCŌĆÖ v├Ā H l├Ā trung ─æiß╗ām BŌĆÖCŌĆÖ.
Mß║Ęt kh├Īc, AH ŌŖź BŌĆÖCŌĆÖ n├¬n AAŌĆÖ ŌŖź BŌĆÖCŌĆÖ. Kß║╗ ─æŲ░ß╗Øng cao HK cß╗¦a tam gi├Īc AAŌĆÖH th├¼ HK ch├Łnh l├Ā khoß║Żng c├Īch giß╗»a AAŌĆÖ v├Ā BŌĆÖCŌĆÖ. Do AAŌĆÖ.HK = AH.AŌĆÖH n├¬n \(HK = \frac{{\frac{a}{2}.\frac{{a\sqrt 3 }}{2}}}{a} = \frac{{a\sqrt 3 }}{4}\)
B├Āi 31 trang 117 SGK H├¼nh hß╗Źc 11 n├óng cao
Cho h├¼nh lß║Łp phŲ░ŲĪng ABCD.AŌĆÖBŌĆÖCŌĆÖDŌĆÖ c├│ cß║Īnh bß║▒ng a. T├Łnh khoß║Żng c├Īch giß╗»a hai ─æŲ░ß╗Øng thß║│ng BCŌĆÖ v├Ā CDŌĆÖ
HŲ░ß╗øng dß║½n giß║Żi:
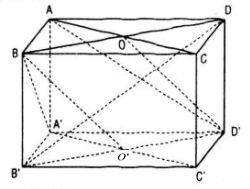
Gß╗Źi O, OŌĆÖ lß║¦n lŲ░ß╗Żt l├Ā t├óm c├Īc h├¼nh vu├┤ng ABCD, AŌĆÖBŌĆÖCŌĆÖDŌĆÖ cß╗¦a h├¼nh lß║Łp phŲ░ŲĪng ABCD.AŌĆÖBŌĆÖCŌĆÖDŌĆÖ cß║Īnh a.
* Ta chß╗®ng minh BŌĆÖD ŌŖź (BAŌĆÖC) v├Ā BŌĆÖD ŌŖź (ACDŌĆÖ)
Ta c├│: \(\left\{ \begin{array}{l}
A\prime C\prime \bot B\prime D\prime \\
A\prime C\prime \bot BB\prime
\end{array} \right. \Rightarrow A\prime C\prime \bot (BB\prime D\prime D)\)
M├Ā BŌĆÖD ŌŖé (BBŌĆÖDŌĆÖD) n├¬n BŌĆÖD ŌŖź AŌĆÖCŌĆÖ (1)
TŲ░ŲĪng tß╗▒ \(\left\{ \begin{array}{l}
AB\prime \bot A\prime B\\
A\prime B \bot B\prime C\prime
\end{array} \right. \Rightarrow A\prime B \bot (AB\prime C\prime D)\)
M├Ā BŌĆÖD ŌŖé (ABŌĆÖCŌĆÖD) n├¬n BŌĆÖD ŌŖź AŌĆÖB (2)
Tß╗½ (1) v├Ā (2) suy ra BŌĆÖD ŌŖź (BAŌĆÖCŌĆÖ)
TŲ░ŲĪng tß╗▒ ta c┼®ng chß╗®ng minh ─æŲ░ß╗Żc BŌĆÖD ŌŖź (ACDŌĆÖ)
* Hai mß║Ęt phß║│ng (BAŌĆÖCŌĆÖ) v├Ā (ACDŌĆÖ) song song vß╗øi nhau, vu├┤ng g├│c vß╗øi ─æoß║Īn BŌĆÖD v├Ā chia BŌĆÖD th├Ānh 3 phß║¦n bß║▒ng nhau (x├®t h├¼nh b├¼nh h├Ānh BBŌĆÖDDŌĆÖ v├Ā BO // DŌĆÖO')
Do ─æ├│ khoß║Żng c├Īch giß╗»a mp(BAŌĆÖC) v├Ā mp(ACDŌĆÖ) l├Ā \(\frac{{B\prime D}}{3} = \frac{{a\sqrt 3 }}{3}\)
* Khoß║Żng c├Īch giß╗»a BCŌĆÖ v├Ā CDŌĆÖ
Khoß║Żng c├Īch giß╗»a hai ─æŲ░ß╗Øng thß║│ng ch├®o nhau BCŌĆÖ v├Ā CDŌĆÖ bß║▒ng khoß║Żng c├Īch giß╗»a hai mß║Ęt phß║│ng song song : mp(BAŌĆÖCŌĆÖ) v├Ā mp(ACDŌĆÖ).
Vß║Ły khoß║Żng c├Īch ─æ├│ l├Ā \(\frac{{a\sqrt 3 }}{3}\)
B├Āi 32 trang 117 SGK H├¼nh hß╗Źc 11 n├óng cao
Cho h├¼nh hß╗Öp chß╗» nhß║Łt ABCD.AŌĆÖBŌĆÖCŌĆÖDŌĆÖ c├│ AB = AAŌĆÖ = a, ACŌĆÖ = 2a.
a. T├Łnh khoß║Żng c├Īch tß╗½ ─æiß╗ām D ─æß║┐n mß║Ęt phß║│ng (ACDŌĆÖ)
b. T├¼m ─æŲ░ß╗Øng vu├┤ng g├│c chung cß╗¦a c├Īc ─æŲ░ß╗Øng thß║│ng ACŌĆÖ v├Ā CDŌĆÖ. T├Łnh khoß║Żng c├Īch giß╗»a hai ─æŲ░ß╗Øng thß║│ng ß║źy.
HŲ░ß╗øng dß║½n giß║Żi:
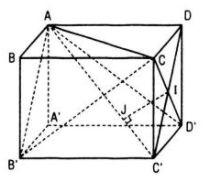
Câu a:
X├®t tß╗® diß╗ćn DACDŌĆÖ c├│ DA, DC, DDŌĆÖ ─æ├┤i mß╗Öt vu├┤ng g├│c n├¬n khoß║Żng c├Īch DH tß╗½ D ─æß║┐n mß║Ęt phß║│ng (ACDŌĆÖ) ─æŲ░ß╗Żc t├Łnh bß╗¤i hß╗ć thß╗®c:
\(\frac{1}{{D{H^2}}} = \frac{1}{{D{A^2}}} + \frac{1}{{D{C^2}}} + \frac{1}{{D{D^{\prime 2}}}}\)
Ta c├│: DC = a. DDŌĆÖ = a
\(AC{\prime ^2} = A{C^2} + CC{\prime ^2} = D{A^2} + D{C^2} + CC{\prime ^2}\)
Hay \(4{a^2} = D{A^2} + {a^2} + {a^2}\), tß╗®c l├Ā: \(D{A^2} = 2{a^2}\)
Vß║Ły \(\frac{1}{{D{H^2}}} = \frac{1}{{2{a^2}}} + \frac{1}{{{a^2}}} + \frac{1}{{{a^2}}} = \frac{5}{{2{a^2}}}\)
Do đó: \(DH = \frac{{a\sqrt {10} }}{5}\)
Câu b:
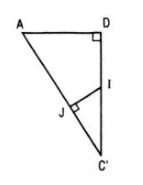
V├¼ CD = DDŌĆÖ = a n├¬n CDŌĆÖ ŌŖź CŌĆÖD. Mß║Ęt kh├Īc AD ŌŖź (CDDŌĆÖCŌĆÖ) n├¬n CDŌĆÖ ŌŖź ACŌĆÖ v├Ā CDŌĆÖ ŌŖź mp(ACŌĆÖD). Gß╗Źi giao ─æiß╗ām cß╗¦a CDŌĆÖ vß╗øi mp(ACŌĆÖD) l├Ā I. Trong mp(ACŌĆÖD) kß║╗ IJ vu├┤ng g├│c vß╗øi ACŌĆÖ tß║Īi J th├¼ IJ l├Ā ─æŲ░ß╗Øng vu├┤ng g├│c chung cß╗¦a ACŌĆÖ v├Ā CDŌĆÖ.
Ta t├Łnh khoß║Żng c├Īch giß╗»a ACŌĆÖ v├Ā CDŌĆÖ
Ta c├│: ╬öCŌĆÖJI ─æß╗ōng dß║Īng ╬öCŌĆÖDA n├¬n \(\frac{{IJ}}{{AD}} = \frac{{IC\prime }}{{AC\prime }}\)
Suy ra: \(IJ = AD.\frac{{C\prime D}}{{2AC\prime }}\)
Mß║Ęt kh├Īc \(C'D = a\sqrt 2 \) n├¬n \(IJ = a\sqrt 2 .\frac{{a\sqrt 2 }}{{2.2a}} = \frac{a}{2}\)
B├Āi 33 trang 118 SGK H├¼nh hß╗Źc 11 n├óng cao
Cho h├¼nh hß╗Öp thoi ABCD.AŌĆÖBŌĆÖCŌĆÖDŌĆÖ c├│ c├Īc cß║Īnh ─æß╗üu bß║▒ng a v├Ā \(\widehat {BAD} = \widehat {BAA\prime } = \widehat {DAA\prime } = {60^0}\). T├Łnh khoß║Żng c├Īch giß╗»a hai mß║Ęt phß║│ng ─æ├Īy (ABCD) v├Ā (AŌĆÖBŌĆÖCŌĆÖDŌĆÖ)
HŲ░ß╗øng dß║½n giß║Żi:
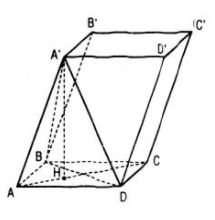
Tß╗½ giß║Ż thiß║┐t suy ra c├Īc tam gi├Īc AŌĆÖAD, BAD, AŌĆÖAB l├Ā c├Īc tam gi├Īc c├ón c├╣ng c├│ g├│c ß╗¤ ─æß╗ēnh bß║▒ng 600 n├¬n ch├║ng l├Ā c├Īc tam gi├Īc ─æß╗üu. NhŲ░ vß║Ły tß╗® diß╗ćn AŌĆÖABD c├│ c├Īc cß║Īnh c├╣ng bß║▒ng a hay AŌĆÖABD l├Ā tß╗® diß╗ćn ─æß╗üu. Khi ─æ├│ h├¼nh chiß║┐u cß╗¦a AŌĆÖ tr├¬n mp(ABCD) ch├Łnh l├Ā trß╗Źng t├óm H cß╗¦a tam gi├Īc ─æß╗üu ABD. Khoß║Żng c├Īch giß╗»a hai mß║Ęt phß║│ng ─æ├Īy (ABCD) v├Ā (AŌĆÖBŌĆÖCŌĆÖDŌĆÖ) ch├Łnh l├Ā ─æß╗Ö d├Āi AŌĆÖH. Ta c├│:
\(\begin{array}{l}
A\prime {H^2} = AA{\prime ^2} - A{H^2}\\
= {a^2} - {\left( {\frac{{a\sqrt 3 }}{3}} \right)^2} = {a^2} - \frac{{{a^2}}}{3} = \frac{{2{a^2}}}{3}
\end{array}\)
Vß║Ły \(A\prime H = \frac{{a\sqrt 6 }}{3}\)
B├Āi 34 trang 118 SGK H├¼nh hß╗Źc 11 n├óng cao
Cho h├¼nh ch├│p S.ABCD c├│ ─æ├Īy l├Ā h├¼nh chß╗» nhß║Łt v├Ā Ab = 2a, BC = a. C├Īc cß║Īnh b├¬n cß╗¦a h├¼nh ch├│p bß║▒ng nhau v├Ā bß║▒ng \(a\sqrt 2 \)
a. T├Łnh khoß║Żng c├Īch tß╗½ S ─æß║┐n mß║Ęt phß║│ng ─æ├Īy (ABCD).
b. Gß╗Źi E v├Ā F lß║¦n lŲ░ß╗Żt l├Ā trung ─æiß╗ām c├Īc cß║Īnh AB v├Ā CD ; K l├Ā ─æiß╗ām bß║źt k├¼ thuß╗Öc ─æŲ░ß╗Øng thß║│ng AD. Chß╗®ng minh rß║▒ng khoß║Żng c├Īch giß╗»a hai ─æŲ░ß╗Øng thß║│ng EF v├Ā SK kh├┤ng phß╗ź thuß╗Öc v├Āo K, h├Ży t├Łnh khoß║Żng c├Īch ─æ├│ theo a.
HŲ░ß╗øng dß║½n giß║Żi:
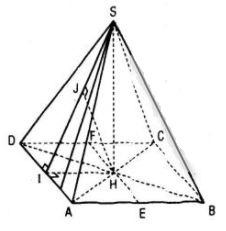
Câu a:
V├¼ SA = SB = SC = SD = \(a\sqrt 2 \) n├¬n h├¼nh chiß║┐u cß╗¦a ─æiß╗ām S tr├¬n mß║Ęt phß║│ng (ABCD) l├Ā ─æiß╗ām H m├Ā HA = HB = HC = HD. Do ABCD l├Ā h├¼nh chß╗» nhß║Łt n├¬n H ch├Łnh l├Ā giao ─æiß╗ām cß╗¦a AC v├Ā BD. Khoß║Żng c├Īch tß╗½ S ─æß║┐n mp(ABCD) bß║▒ng SH. Ta c├│:
\(\begin{array}{l}
S{H^2} = S{A^2} - \frac{{A{C^2}}}{4} = 2{a^2} - \frac{{A{B^2} + B{C^2}}}{4}\\
= 2{a^2} - \frac{{4{a^2} + {a^2}}}{4} = \frac{{3{a^2}}}{4}\\
\Rightarrow SH = \frac{{a\sqrt 3 }}{2}
\end{array}\)
Câu b:
V├¼ EF // AD n├¬n EF // mp(SAD), mß║Ęt kh├Īc SK nß║▒m trong mp(SAD) n├¬n khoß║Żng c├Īch giß╗»a EF v├Ā SK ch├Łnh l├Ā khoß║Żng c├Īch giß╗»a EF v├Ā mp(SAD), ─æ├│ c┼®ng ch├Łnh l├Ā khoß║Żng c├Īch tß╗½ H ─æß║┐n mp(SAD). Vß║Ły khoß║Żng c├Īch giß╗»a EF v├Ā SK kh├┤ng phß╗ź thuß╗Öc v├Āo vß╗ŗ tr├Ł cß╗¦a ─æiß╗ām K tr├¬n ─æŲ░ß╗Øng thß║│ng AD.
T├Łnh d(EF ; SK) :
Gß╗Źi I l├Ā trung ─æiß╗ām cß╗¦a AD, kß║╗ ─æŲ░ß╗Øng cao HJ cß╗¦a tam gi├Īc vu├┤ng SHI th├¼ HJ ŌŖź mp(SAD), do ─æ├│ d(H; (SAD)) = HJ. Ta c├│: HJ.SI = SH.HI
\(\begin{array}{l}
S{I^2} = S{A^2} - A{I^2} = 2{a^2} - \frac{{{a^2}}}{4} = \frac{{7{a^2}}}{4}\\
\Rightarrow HJ = \frac{{SH.HI}}{{SI}} = \frac{{\frac{{a\sqrt 3 }}{2}.a}}{{\frac{{a\sqrt 7 }}{2}}} = \frac{{a\sqrt {21} }}{7}
\end{array}\)
Vß║Ły khoß║Żng c├Īch giß╗»a EF v├Ā SK kh├┤ng phß╗ź thuß╗Öc v├Āo vß╗ŗ tr├Ł cß╗¦a ─æiß╗ām K tr├¬n ─æŲ░ß╗Øng thß║│ng AD v├Ā bß║▒ng \(\frac{{a\sqrt {21} }}{7}\)
B├Āi 35 trang 118 SGK H├¼nh hß╗Źc 11 n├óng cao
Cho tß╗® diß╗ćn ABCD. Chß╗®ng minh rß║▒ng nß║┐u AC = BD, AD = BC th├¼ ─æŲ░ß╗Øng vu├┤ng g├│c chung cß╗¦a AB v├Ā CD l├Ā ─æŲ░ß╗Øng thß║│ng nß╗æi trung ─æiß╗ām cß╗¦a AB v├Ā CD. ─Éiß╗üu ngŲ░ß╗Żc lß║Īi c├│ ─æ├║ng kh├┤ng ?
HŲ░ß╗øng dß║½n giß║Żi:
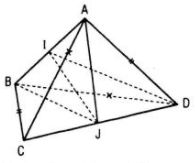
Câu a:
V├¼ AC = BD, AD = BC n├¬n tam gi├Īc ACD bß║▒ng tam gi├Īc BDC, tß╗½ ─æ├│ hai trung tuyß║┐n tŲ░ŲĪng ß╗®ng AJ v├Ā BJ bß║▒ng nhau (ß╗¤ ─æ├│ J l├Ā trung ─æiß╗ām cß╗¦a CD). Gß╗Źi I l├Ā trung ─æiß╗ām cß╗¦a AB th├¼ ta c├│ JI ŌŖź AB.
TŲ░ŲĪng tß╗▒ nhŲ░ tr├¬n ta c┼®ng c├│ JI ŌŖź CD. Vß║Ły JI l├Ā ─æŲ░ß╗Øng vu├┤ng g├│c chung cß╗¦a AB v├Ā CD.
Câu b:
─Éiß╗üu ngŲ░ß╗Żc lß║Īi cß╗¦a kß║┐t luß║Łn n├¬u ra trong b├Āi to├Īn c┼®ng ─æ├║ng, tß╗®c l├Ā nß║┐u IJ ŌŖź AB, IJ ŌŖź CD, I, J lß║¦n lŲ░ß╗Żt l├Ā trung ─æiß╗ām cß╗¦a AB v├Ā CD th├¼ AC = BD; AD = BC.
Thß║Łt vß║Ły, v├¼ IJ ŌŖź AB, I l├Ā trung ─æiß╗ām cß╗¦a AB n├¬n AJ = BJ. Mß║Ęt kh├Īc:
\(\begin{array}{l}
A{C^2} + A{D^2} = 2A{J^2} + \frac{{C{D^2}}}{2}\\
B{C^2} + B{D^2} = 2B{J^2} + \frac{{C{D^2}}}{2}\\
\Rightarrow A{C^2} + A{D^2} = B{C^2} + B{D^2}\left( 1 \right)
\end{array}\)
TŲ░ŲĪng tß╗▒ nhŲ░ tr├¬n ta c┼®ng c├│: \(C{B^2} + C{A^2} = D{B^2} + D{A^2}(2)\)
Tß╗½ (1) v├Ā (2) ta suy ra \(A{D^2} - B{C^2} = B{C^2} - D{A^2}\), tß╗®c l├Ā DA = BC v├Ā tß╗½ (1) ta c┼®ng c├│ AC = BD.
Tr├¬n ─æ├óy l├Ā nß╗Öi dung hŲ░ß╗øng dß║½n giß║Żi chi tiß║┐t b├Āi tß║Łp SGK n├óng cao m├┤n H├¼nh hß╗Źc 11 ChŲ░ŲĪng 3 B├Āi 5 Khoß║Żng c├Īch ─æŲ░ß╗Żc tr├¼nh b├Āy r├Ą r├Āng, cß╗ź thß╗ā vß╗øi phŲ░ŲĪng ph├Īp ngß║»n gß╗Źn v├Ā khoa hß╗Źc. Hy vß╗Źng rß║▒ng ─æ├óy sß║Į l├Ā t├Āi liß╗ću hß╗»u ├Łch gi├║p c├Īc em hß╗Źc sinh lß╗øp 11 hß╗Źc tß║Łp thß║Łt tß╗æt!
T├Āi liß╗ću li├¬n quan
TŲ░ liß╗ću nß╗Ģi bß║Łt tuß║¦n
- Xem thêm












