Giải Toán 11 SGK nâng cao Chương 1 Bài 3 Một số dạng phương trình lượng giác đơn giản

Giải các phương trình sau:

a) $2\cos x - \sqrt 3  = 0$

b) $\sqrt 3 \tan 3x - 3 = 0$

c) $\left( {\sin x + 1} \right)\left( {2\cos 2x - \sqrt 2 } \right) = 0$

Hướng dẫn giải:

Câu a:

$\begin{array}{l} 2\cos x - \sqrt 3  = 0 \Leftrightarrow \cos x = \frac{{\sqrt 3 }}{2} \Leftrightarrow \cos x = \cos \frac{\pi }{6}\\  \Leftrightarrow x =  \pm \frac{\pi }{6} + k2\pi ,k \in Z \end{array}$

Câu b:

$\begin{array}{l} \sqrt 3 \tan 3x - 3 = 0 \Leftrightarrow \tan 3x = \sqrt 3  \Leftrightarrow \tan 3x = \tan \frac{\pi }{3}\\  \Leftrightarrow 3x = \frac{\pi }{3} + k\pi  \Leftrightarrow x = \frac{\pi }{9} + k\frac{\pi }{3},k \in Z \end{array}$

Câu c:

$\begin{array}{l} \left( {\sin x + 1} \right)\left( {2\cos 2x - \sqrt 2 } \right) = 0\\  \Leftrightarrow \left[ \begin{array}{l} \sin x + 1 = 0\\ 2\cos 2x - \sqrt 2  = 0 \end{array} \right. \Leftrightarrow \left[ \begin{array}{l} \sin x =  - 1\\ \cos 2x = \frac{{\sqrt 2 }}{2} \end{array} \right.\\  \Leftrightarrow \left[ \begin{array}{l} x =  - \frac{\pi }{2} + k2\pi \\ 2x =  \pm \frac{\pi }{4} + k2\pi  \end{array} \right. \Leftrightarrow \left[ \begin{array}{l} x =  - \frac{\pi }{2} + k2\pi \\ x =  \pm \frac{\pi }{8} + k\pi  \end{array} \right. \end{array}$

---

Giải các phương trình sau:

a) $2{\cos ^2}x - 3\cos x + 1 = 0$

b) ${\cos ^2}x + \sin x + 1 = 0$

c) $\sqrt 3 {\tan ^2}x - \left( {1 + \sqrt 3 } \right)\tan x + 1 = 0$

Hướng dẫn giải:

Câu a:

Đặt $t = \cos x,\left| t \right| \le 1$, ta có:

$2{t^2} - 3t + 1 = 0 \Leftrightarrow \left[ \begin{array}{l} t = 1\\ t = \frac{1}{2} \end{array} \right. \Leftrightarrow \left[ \begin{array}{l} \cos x = 1\\ \cos x = \frac{1}{2} \end{array} \right. \Leftrightarrow \left[ \begin{array}{l} x = k2\pi \\ x =  \pm \frac{\pi }{3} + k2\pi  \end{array} \right.\left( {k \in Z} \right)$

Câu b:

$\begin{array}{l} {\cos ^2}x + \sin x + 1 = 0 \Leftrightarrow 1 - {\sin ^2}x + \sin x + 1 = 0\\  \Leftrightarrow {\sin ^2}x - \sin x - 2 = 0\\  \Leftrightarrow \left[ \begin{array}{l} \sin x =  - 1\\ \sin x = 2\left( l \right) \end{array} \right. \Leftrightarrow x =  - \frac{\pi }{2} + k2\pi  \end{array}$

Câu c:

$\begin{array}{l} \sqrt 3 {\tan ^2}x - \left( {1 + \sqrt 3 } \right)\tan x + 1 = 0\\  \Leftrightarrow \left[ \begin{array}{l} \tan x = 1\\ \tan x = \frac{1}{{\sqrt 3 }} \end{array} \right. \Leftrightarrow \left[ \begin{array}{l} x = \frac{\pi }{4} + k\pi \\ x = \frac{\pi }{6} + k\pi  \end{array} \right.\left( {k \in Z} \right) \end{array}$

---

Giải các phương trình sau trên khoảng đã cho rồi dùng bảng số hoặc máy tính bỏ túi để tính gần đúng nghiệm của chúng (tính chính xác đến hàng phần trăm):

a.  $3\cos 2x + 10\sin x + 1 = 0$ trên $\left( { - \frac{\pi }{2};\frac{\pi }{2}} \right)$

b.  $4\cos 2x + 3 = 0$ trên $\left( {0;\frac{\pi }{2}} \right)$

c.  ${\cot ^2}x - 3\cot x - 10 = 0$ trên (0;π)

d.  5−3tan3x = 0 trên $\left( { - \frac{\pi }{6};\frac{\pi }{6}} \right)$

Hướng dẫn giải:

Câu a:

Ta có:

$3\cos 2x + 10\sin x + 1 = 0 \Leftrightarrow  - 6{\sin ^2}x + 6\sin x + 4 = 0 \Leftrightarrow \left[ \begin{array}{l} \sin x =  - \frac{1}{3}\\ \sin x = 2\left( l \right) \end{array} \right.$

Phương trình $\sin x =  - \frac{1}{3}$ có nghiệm gần đúng là $x \approx  - 0,34$

Câu b:

Ta thấy $0 < x < \frac{\pi }{2} \Leftrightarrow 0 < 2x < \pi$. Với điều kiện đó, ta có:

$4\cos 2x + 3 = 0 \Leftrightarrow \cos 2x =  - \frac{3}{4} \Leftrightarrow 2x = \alpha  \Leftrightarrow x = \frac{\alpha }{2}$, trong đó α là số thực thuộc khoảng (0;π) thỏa mãn $\cos \alpha  =  - \frac{3}{4}$. Dùng bảng số hoặc máy tính, ta tìm được $\alpha  \approx 2,42$. Từ đó nghiệm gần đúng của phương trình là $x = \frac{\alpha }{2} \approx 1,21$

Câu c:

${\cot ^2}x - 3\cot x - 10 = 0 \Leftrightarrow \left[ \begin{array}{l} \cot x = 5\\ \cot x =  - 2 \end{array} \right.$

Nghiệm gần đúng của phương trình trong khoảng (0;π) là $x \approx 0,2;x \approx 2,68$

Câu d:

$x \in \left( { - \frac{\pi }{6};\frac{\pi }{6}} \right) \Leftrightarrow 3x \in \left( { - \frac{\pi }{2};\frac{\pi }{2}} \right)$. Với điều kiện đó, ta có:

$5 - 3\tan 3x = 0 \Leftrightarrow \tan 3x = \frac{5}{3} \Leftrightarrow 3x = \beta  \Leftrightarrow x = \frac{\beta }{3}$, 

Trong đó β là số thực thuộc khoảng $\left( { - \frac{\pi }{2};\frac{\pi }{2}} \right)$ thỏa mãn $\tan \beta  = \frac{5}{3}$; bảng số hoặc máy tính cho ta $\beta  \approx 1,03$. Vậy nghiệm gần đúng của phương trình là $x \approx 0,34$.

---

Giải các phương trình sau:

a) $3\cos x + 4\sin x =  - 5$

b) $2\sin 2x - 2\cos 2x = \sqrt 2$

c) $5\sin 2x - 6{\cos ^2}x = 13$

Hướng dẫn giải:

Câu a:

Chia 2 vế phương trình cho $\sqrt {{3^2} + {4^2}}  = 5$ ta được:

$\frac{3}{5}\cos x + \frac{4}{5}\sin x =  - 1 \Leftrightarrow \cos x\cos \alpha  + \sin x\sin \alpha  =  - 1$ (trong đó $\cos \alpha  = \frac{3}{5},\sin \alpha  = \frac{4}{5}$)

$\Leftrightarrow \cos \left( {x - \alpha } \right) =  - 1 \Leftrightarrow x - \alpha  = \pi  + k2\pi  \Leftrightarrow x = \pi  + \alpha  + k2\pi ,k \in Z$

Câu b:

Chia 2 vế phương trình cho $\sqrt {{2^2} + {2^2}}  = 2\sqrt 2$ ta được:

$\begin{array}{l} \frac{1}{{\sqrt 2 }}\sin 2x - \frac{1}{{\sqrt 2 }}\cos 2x = \frac{1}{2} \Leftrightarrow \sin 2x\cos \frac{\pi }{4} - \cos 2x\sin \frac{\pi }{4} = \frac{1}{2}\\  \Leftrightarrow \sin \left( {2x - \frac{\pi }{4}} \right) = \frac{1}{2} \Leftrightarrow \left[ \begin{array}{l} 2x - \frac{\pi }{4} = \frac{\pi }{6} + k2\pi \\ 2x - \frac{\pi }{4} = \pi  - \frac{\pi }{6} + k2\pi  \end{array} \right. \Leftrightarrow \left[ \begin{array}{l} x = \frac{{5\pi }}{{24}} + k\pi \\ x = \frac{{13\pi }}{{24}} + k\pi  \end{array} \right.\left( {k \in Z} \right) \end{array}$

Câu c:

$\begin{array}{l} 5\sin 2x - 6{\cos ^2}x = 13 \Leftrightarrow 5\sin 2x - 3\left( {1 + \cos 2x} \right) = 13\\  \Leftrightarrow 5\sin 2x - 3\cos 2x = 16 \end{array}$

Chia 2 vế cho ta được:

$\frac{5}{{\sqrt {34} }}\sin 2x - \frac{3}{{\sqrt {34} }}\cos 2x = \frac{{16}}{{\sqrt {34} }}$

Do ${\left( {\frac{5}{{\sqrt {34} }}} \right)^2} + {\left( {\frac{3}{{\sqrt {34} }}} \right)^2} = 1$ nên ta chọn được số $\alpha$ sao cho $\cos \alpha  = \frac{5}{{\sqrt {34} }},\sin \alpha  = \frac{3}{{\sqrt {34} }}$

Do đó $5\sin 2x - 6{\cos ^2}x = 13 \Leftrightarrow \sin \left( {2x - \alpha } \right) = \frac{{16}}{{\sqrt {34} }} > 1$

Vậy phương trình đã cho vô nghiệm.

---

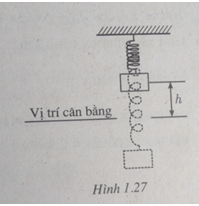
Một vật nặng treo bởi một chiếc lò xo chuyển động lên xuống qua vị trí cân bằng. Khoảng cách h từ vật đó đến vị trí cân bằng ở thời điểm t giây được tính theo công thức h = |d| trong đó d = 5sin6t–4cos6t với d được tính bằng xentimet, ta quy ước rằng d > 0 khi vật ở phía trên vị trí cân bằng, d < 0 khi vật ở phía dưới vị trí cân bằng. Hỏi:

a. Ở thời điểm nào trong 1 giây đầu tiên, vật ở vị trí cân bằng?

b. Ở thời điểm nào trong 1 giây đầu tiên, vật ở xa vị trí cân bằng nhất?

(Tính chính xác đến $\frac{1}{{100}}$ giây).

Hướng dẫn giải:

Ta có $5\sin 6t - 4cos6t = \sqrt {41} \left( {\frac{5}{{\sqrt {41} }}\sin 6t - \frac{4}{{\sqrt {41} }}\cos 6t} \right) = \sqrt {41} \sin \left( {6t - \alpha } \right)$, trong đó số α được chọn sao cho $\cos \alpha  = \frac{5}{{\sqrt {41} }}$ và $\sin \alpha  = \frac{4}{{\sqrt {41} }}$. Sử dụng bảng số hoặc máy tính bỏ túi, ta chọn được $\alpha  \approx 0,675$.

Câu a:

Vật ở vị trí cân bằng khi d = 0, nghĩa là sin(6t–α) = 0

$\Leftrightarrow t = \frac{\alpha }{6} + k\frac{\pi }{6},k \in Z$

Ta cần tìm k nguyên dương sao cho 0 ≤ t ≤ 1

$0 \le t \le 1 \Leftrightarrow 0 \le \frac{\alpha }{6} + k\frac{\pi }{6} \le 1 \Leftrightarrow  - \frac{\alpha }{\pi } \le k \le \frac{{6 - \alpha }}{\pi }$

Với $\alpha  \approx 0,675$, ta thu được −0,215 < k < 1,7 nghĩa là $k \in \left\{ {0;1} \right\}$. Vậy trong khoảng 1 giây đầu tiên, có hai thời điểm vật ở vị trí cân bằng là:

$t \approx \frac{\alpha }{6} \approx 0,11$ (giây) và $t = \frac{\alpha }{6} + \frac{\pi }{6} \approx 0,64$ (giây)

Câu b:

Vật ở xa vị trí cân bằng nhất khi và chỉ khi |d| nhận giá trị lớn nhất.

Điều đó xảy ra nếu sin(6t–α) = ±1. Ta có:

$\sin \left( {6t - \alpha } \right) =  \pm 1 \Leftrightarrow \cos \left( {6t - \alpha } \right) = 0 \Leftrightarrow t = \frac{\alpha }{6} + \frac{\pi }{{12}} + k\frac{\pi }{6}$

Ta tìm k nguyên dương sao cho 0 ≤ t ≤ 1

$\begin{array}{*{20}{l}} {0 \le t \le 1 \Leftrightarrow 0 \le \frac{\alpha }{6} + \frac{\pi }{{12}} + k\frac{\pi }{6} \le 1}\\ { \Leftrightarrow  - \frac{\alpha }{\pi } - \frac{1}{2} \le k \le \frac{{6 - \alpha }}{\pi } - \frac{1}{2}} \end{array}$

Với $\alpha  \approx 0,675$, ta thu được −0,715 < k < 1,2; nghĩa là k ∈ {0;1}. Vậy trong khoảng 1 giây đầu tiên, có hai thời điểm vật ở xa vị trí cân bằng nhất là:

$t = \frac{\alpha }{6} + \frac{\pi }{{12}} \approx 0,37$ (giây) và $t = \frac{\alpha }{6} + \frac{\pi }{{12}} + \frac{\pi }{6} \approx 0,90$ (giây)

---

Tìm giá trị lớn nhất và giá trị nhỏ nhất của mỗi biểu thức sau:

a. asinx+bcosx (a và b là hằng số, a²+b² ≠ 0) ;

b.  sin²x+sinxcosx+3cos²x;

c.Asin²x+Bsinxcosx+Ccos²x (A, B và C là hằng số).

Hướng dẫn giải:

Câu a:

Ta có:

$\begin{array}{l} a\sin x + b\cos x = \sqrt {{a^2} + {b^2}} \left( {\frac{a}{{\sqrt {{a^2} + {b^2}} }}\sin x + \frac{b}{{\sqrt {{a^2} + {b^2}} }}\cos x} \right)\\  = \sqrt {{a^2} + {b^2}} \left( {\sin x\cos \alpha  + \sin \alpha \cos x} \right) = \sqrt {{a^2} + {b^2}} \sin \left( {x + \alpha } \right) \end{array}$ (trong đó $\sin \alpha  = \frac{b}{{\sqrt {{a^2} + {b^2}} }},\cos \alpha  = \frac{a}{{\sqrt {{a^2} + {b^2}} }}$) 

Giá trị lớn nhất và giá trị nhỏ nhất của asinx+bcosxx lần lượt là:

$\sqrt {{a^2} + {b^2}}$ và $- \sqrt {{a^2} + {b^2}}$

Câu b:

Ta có:

$\begin{array}{l} {\sin ^2}x + \sin x\cos x + 3{\cos ^2}x = \frac{1}{2}\sin 2x + \frac{{1 - \cos 2x}}{2} + 3.\frac{{1 + \cos 2x}}{2}\\  = \frac{1}{2}\sin 2x + \cos 2x + 2 \end{array}$

Ta có $\left| {\frac{1}{2}\sin 2x + \cos 2x} \right| \le \sqrt {{{\left( {\frac{1}{2}} \right)}^2} + {1^2}}  = \frac{{\sqrt 5 }}{2}$

Do đó giá trị lớn nhất và giá trị nhỏ nhất của sin²x+sinxcosx+3cos²x lần lượt là:  

$\frac{{\sqrt 5 }}{2} + 2, - \frac{{\sqrt 5 }}{2} + 2$

Câu c:

Ta có:

$\begin{array}{l} A{\sin ^2}x + B\sin x\cos x + C{\cos ^2}x\\  = A.\frac{{1 - \cos 2x}}{2} + \frac{B}{2}.\sin 2x + C.\frac{{1 + \cos 2x}}{2}\\  = \frac{B}{2}.\sin 2x + \frac{{C - A}}{2}.\cos 2x + \frac{{C + A}}{2} = a\sin 2x + b\cos 2x + c \end{array}$

trong đó $a = \frac{B}{2},b = \frac{{C - A}}{2},c = \frac{{C + A}}{2}$

Vậy Asin²x+Bsinxcosx+Ccos²x đạt giá trị lớn nhất là:

$\sqrt {{a^2} + {b^2}}  + c = \sqrt {\frac{{{B^2} + {{\left( {C - A} \right)}^2}}}{4}}  + \frac{{C + A}}{2} = \frac{1}{2}\sqrt {{B^2} + \left( {C - A} \right)}  + \frac{{C + A}}{2}$ và giá trị nhỏ nhất là $- \frac{1}{2}\sqrt {{B^2} + {{\left( {C - A} \right)}^2}}  + \frac{{C + A}}{2}$.

---

Giải các phương trình sau:

a.  $2{\sin ^2}x + 3\sqrt 3 \sin x\cos x - {\cos ^2}x = 4$

b.  $3{\sin ^2}x + 4\sin 2x + \left( {8\sqrt 3  - 9} \right){\cos ^2}x = 0$

c.  ${\sin ^2}x + \sin 2x - 2{\cos ^2}x = \frac{1}{2}$

Hướng dẫn giải:

Câu a:

cosx = 0 không thỏa mãn phương trình.

Chia hai vế phương trình cho cos²x ≠ 0 ta được:

$\begin{array}{l} 2{\tan ^2}x + 3\sqrt 3 \tan x - 1 = 4\left( {1 + {{\tan }^2}x} \right)\\  \Leftrightarrow 2{\tan ^2}x - 3\sqrt 3 \tan x + 5 = 0 \end{array}$

Phương trình vô nghiệm nên phương trình đã cho vô nghiệm.

Câu b:

Các giá trị của x mà cosx = 0 không là nghiệm phương trình.

Chia hai vế phương trình cho cos²x ta được:

$\begin{array}{l} 3{\tan ^2}x + 8\tan x + 8\sqrt 3  - 9 = 0 \Leftrightarrow \left[ \begin{array}{l} \tan x =  - \sqrt 3 \\ \tan x =  - \frac{8}{3} + \sqrt 3  \end{array} \right.\\  \Leftrightarrow \left[ \begin{array}{l} x = \frac{\pi }{3} + k\pi \\ x = \alpha  + k\pi  \end{array} \right.\left( {k \in Z} \right) \end{array}$

trong đó $\tan \alpha  =  - \frac{8}{3} + \sqrt 3$

Câu c:

Các giá trị của x mà cosx = 0 không là nghiệm phương trình.

Chia hai vế phương trình cho cos²x ta được:

$\begin{array}{l} {\tan ^2}x + 2\tan x - 2 = \frac{1}{2}\left( {1 + {{\tan }^2}x} \right)\\  \Leftrightarrow {\tan ^2}x + 4\tan x - 5 = 0 \Leftrightarrow \left[ \begin{array}{l} \tan x = 1\\ \tan x =  - 5 \end{array} \right.\\  \Leftrightarrow \left[ \begin{array}{l} x = \frac{\pi }{4} + k\pi \\ x = \alpha  + k\pi  \end{array} \right.\left( {k \in Z} \right) \end{array}$ 

trong đó $\tan \alpha  =  - 5$

---

Sử dụng công thức biến đổi tổng thành tích hoặc tích thành tổng để giải các phương trình sau:

a) $\cos x\cos 5x = \cos 2x\cos 4x$

b) $\cos 5x\sin 4x = \cos 3x\sin 2x$

c) $\sin 2x + \sin 4x = \sin 6x$

d) $\sin x + \sin 2x = \cos x + \cos 2x$

Hướng dẫn giải:

Câu a:

$\begin{array}{l} \cos x\cos 5x = \cos 2x\cos 4x \Leftrightarrow \frac{1}{2}\left( {\cos 6x + \cos 4x} \right) = \frac{1}{2}\left( {\cos 6x + \cos 2x} \right)\\  \Leftrightarrow \cos 4x = \cos 2x \Leftrightarrow \left[ \begin{array}{l} 4x = 2x + k2\pi \\ 4x =  - 2x + k2\pi  \end{array} \right. \Leftrightarrow \left[ \begin{array}{l} x = k\pi \\ x = k\frac{\pi }{3} \end{array} \right. \Leftrightarrow x = k\frac{\pi }{3}\left( {k \in Z} \right) \end{array}$

Câu b:

$\begin{array}{l} \cos 5x\sin 4x = \cos 3x\sin 2x \Leftrightarrow \frac{1}{2}\left( {\sin 9x - \sin x} \right) = \frac{1}{2}\left( {\sin 5x - \sin x} \right)\\  \Leftrightarrow \sin 9x = \sin 5x \Leftrightarrow \left[ \begin{array}{l} 9x = 5x + k2\pi \\ 9x = \pi  - 5x + k2\pi  \end{array} \right. \Leftrightarrow \left[ \begin{array}{l} x = k\frac{\pi }{2}\\ x = \frac{\pi }{{14}} + k\frac{\pi }{7} \end{array} \right.\left( {k \in Z} \right) \end{array}$

Câu c:

$\begin{array}{l} \sin 2x + \sin 4x = \sin 6x \Leftrightarrow 2\sin 3x\cos x = 2\sin 3x\cos 3x\\  \Leftrightarrow \sin 3x\left( {\cos x - \cos 3x} \right) = 0 \Leftrightarrow \left[ \begin{array}{l} \sin 3x = 0\\ \cos x = \cos 3x \end{array} \right.\\  \Leftrightarrow \left[ \begin{array}{l} x = k\frac{\pi }{3}\\ x = k\pi \\ x = k\frac{\pi }{2} \end{array} \right. \Leftrightarrow \left[ \begin{array}{l} x = k\frac{\pi }{3}\\ x = k\frac{\pi }{2} \end{array} \right.\left( {k \in Z} \right) \end{array}$

Câu d:

$\begin{array}{l} \sin x + \sin 2x = \cos x + \cos 2x \Leftrightarrow 2\sin \frac{{3x}}{2}\cos \frac{x}{2} = 2\cos \frac{{3x}}{2}\cos \frac{x}{2}\\  \Leftrightarrow \cos \frac{x}{2}\left( {\sin \frac{{3x}}{2} - \cos \frac{{3x}}{2}} \right) = 0 \Leftrightarrow \left[ \begin{array}{l} \cos \frac{x}{2} = 0\\ \sin \frac{{3x}}{2} = \cos \frac{{3x}}{2} \end{array} \right.\\  \Leftrightarrow \left[ \begin{array}{l} \frac{x}{2} = \frac{\pi }{2} + k\pi \\ \tan \frac{{3x}}{2} = 1 \end{array} \right. \Leftrightarrow \left[ \begin{array}{l} x = \pi  + k2\pi \\ x = \frac{\pi }{6} + k\frac{{2\pi }}{3} \end{array} \right.\left( {k \in Z} \right) \end{array}$

---

Dùng công thức hạ bậc để giải các phương trình sau:

a) ${\sin ^2}4x + {\sin ^2}3x = {\sin ^2}2x + {\sin ^2}x$

b) ${\cos ^2}x + {\cos ^2}2x + {\cos ^2}3x + {\cos ^2}4x = 2$

Hướng dẫn giải:

Câu a:

$\begin{array}{l} {\sin ^2}4x + {\sin ^2}3x = {\sin ^2}2x + {\sin ^2}x\\  \Leftrightarrow \frac{1}{2}\left( {1 - \cos 8x} \right) + \frac{1}{2}\left( {1 - \cos 6x} \right) = \frac{1}{2}\left( {1 - \cos 4x} \right) + \frac{1}{2}\left( {1 - \cos 2x} \right)\\  \Leftrightarrow \cos 8x + \cos 6x = \cos 4x + \cos 2x\\  \Leftrightarrow \cos 7x\cos x = \cos 3x\cos x\\  \Leftrightarrow \cos x\left( {\cos 7x - \cos 3x} \right) = 0\\  \Leftrightarrow \left[ \begin{array}{l} \cos x = 0\\ \cos 7x = \cos 3x \end{array} \right. \Leftrightarrow \left[ \begin{array}{l} x = \frac{\pi }{2} + k\pi \\ x = k\frac{\pi }{2}\\ x = k\frac{\pi }{5} \end{array} \right. \Leftrightarrow \left[ \begin{array}{l} x = k\frac{\pi }{2}\\ x = k\frac{\pi }{5} \end{array} \right.\left( {k \in Z} \right) \end{array}$

Câu b:

$\begin{array}{l} {\cos ^2}x + {\cos ^2}2x + {\cos ^2}3x + {\cos ^2}4x = 2\\  \Leftrightarrow \frac{{1 + \cos 2x}}{2} + \frac{{1 + \cos 4x}}{2} + \frac{{1 + \cos 6x}}{2} + \frac{{1 + \cos 8x}}{2} = 2\\  \Leftrightarrow \left( {\cos 2x + \cos 4x} \right) + \left( {\cos 6x + \cos 8x} \right) = 0\\  \Leftrightarrow 2\cos 3x\cos x + 2\cos 7x\cos x = 0\\  \Leftrightarrow \cos x\left( {\cos 3x + \cos 7x} \right) = 0\\  \Leftrightarrow 2\cos x\cos 5x\cos 2x = 0\\  \Leftrightarrow \left[ \begin{array}{l} \cos x = 0\\ \cos 2x = 0\\ \cos 5x = 0 \end{array} \right. \Leftrightarrow \left[ \begin{array}{l} x = \frac{\pi }{2} + k\pi \\ x = \frac{\pi }{4} + k\frac{\pi }{2}\\ x = \frac{\pi }{{10}} + k\frac{\pi }{5} \end{array} \right.\left( {k \in Z} \right) \end{array}$

---

Giải các phương trình sau:

a. $\tan \frac{x}{2} = \tan x$

b.  $\tan \left( {2x + {{10}^0}} \right) + \cot x = 0$

c.  $\left( {1 - \tan x} \right)\left( {1 + \sin 2x} \right) = 1 + \tan x$

d.  tanx+tan2x = sin3xcosx

e.  tanx+cot2x = 2cot4x

Hướng dẫn giải:

Câu a:

ĐKXĐ: $\left\{ \begin{array}{l} \cos \frac{x}{2} \ne 0\\ \cos x \ne 0 \end{array} \right.$

Ta có $\tan \frac{x}{2} = \tan x \Leftrightarrow x = \frac{x}{2} + k\pi  \Leftrightarrow x = k2\pi,k\in Z$ (nhận)

Câu b:

ĐKXĐ:  $\left\{ \begin{array}{l} \cos \left( {2x + {{10}^0}} \right) \ne 0\\ \sin x \ne 0 \end{array} \right.$

Ta có:

$\begin{array}{l} \tan \left( {2x + {{10}^0}} \right) + \cot x = 0 \Leftrightarrow \tan \left( {2x + {{10}^0}} \right) = \tan \left( {{{90}^0} + x} \right)\\  \Leftrightarrow 2x + {10^0} = {90^0} + x + k{180^0} \Leftrightarrow x = {80^0} + k{180^0} \end{array}$

Hiển nhiên x = 80⁰+k180⁰ thỏa mãn ĐKXĐ.

Vậy phương trình đã cho có các nghiệm là x = 80⁰+k180⁰

Câu c:

Đặt t = tanx, với điều kiện cosx ≠ 0.

Ta có $\sin 2x = \frac{{2\tan x}}{{1 + {{\tan }^2}x}} = \frac{{2t}}{{1 + {t^2}}}$

Do đó $1 + \sin 2x = 1 + \frac{{2t}}{{1 + {t^2}}} = \frac{{{{\left( {1 + t} \right)}^2}}}{{1 + {t^2}}}$

Vậy ta có phương trình:

$\begin{array}{l} \left( {1 - t} \right)\frac{{{{\left( {1 + t} \right)}^2}}}{{1 + {t^2}}} = 1 + t\\  \Leftrightarrow \left( {1 - t} \right){\left( {1 + t} \right)^2} = \left( {1 + t} \right)\left( {1 + {t^2}} \right)\\  \Leftrightarrow 2{t^2}\left( {1 + t} \right) = 0 \Leftrightarrow \left[ \begin{array}{l} t = 0\\ t =  - 1 \end{array} \right.\\  \Leftrightarrow \left[ \begin{array}{l} \tan x = 0\\ \tan x =  - 1 \end{array} \right. \Leftrightarrow \left[ \begin{array}{l} x = k\pi \\ x =  - \frac{\pi }{4} + k\pi  \end{array} \right.\left( {k \in Z} \right) \end{array}$

Câu d:

ĐKXĐ: cosx ≠ 0 và cos²x ≠ 0. Với điều kiện đó, ta có:

$\begin{array}{l} \tan x + \tan 2x = \sin 3x\cos x\\  \Leftrightarrow \frac{{\sin 3x}}{{\cos x\cos 2x}} = \sin 3x\cos x\\  \Leftrightarrow \sin 3x\left( {\frac{1}{{\cos x\cos 2x}} - \cos x} \right) = 0\\  \Leftrightarrow \left[ \begin{array}{l} \sin 3x = 0\\ \frac{1}{{\cos x\cos 2x}} = \cos x \end{array} \right. \end{array}$

• $\left[ \begin{array}{l} \sin 3x = 0 \Leftrightarrow x = k\frac{\pi }{3}\\ \frac{1}{{\cos x\cos 2x}} = \cos x \end{array} \right.$
• $\begin{array}{l} \frac{1}{{\cos x\cos 2x}} = \cos x \Leftrightarrow {\cos ^2}x\cos 2x = 1 \Leftrightarrow \left( {1 + \cos 2x} \right)\cos 2x = 2\\  \Leftrightarrow {\cos ^2}x + \cos 2x - 2 = 0\\ \cos 2x = 1 \Leftrightarrow x = k\pi  \end{array}$

Vậy phương trình có nghiệm $x = k\frac{\pi }{3}\left( {k \in Z} \right)$

Câu e:

ĐKXĐ: cosx ≠ 0, sin2x ≠ 0 và sin4x ≠ 0. Tuy nhiên chỉ cần sin4x ≠ 0 là đủ (vì sin4x = 2sin2xcos2x = 4sinxcosxcos2x). Với điều kiện đó ta có:

$\begin{array}{l} \tan x + \cot 2x = 2\cot 4x\\  \Leftrightarrow \frac{{\sin x}}{{\cos x}} + \frac{{\cos 2x}}{{\sin 2x}} = \frac{{2\cos 4x}}{{\sin 4x}}\\  \Leftrightarrow \frac{{\sin x\sin 2x + \cos x\cos 2x}}{{\cos x\sin 2x}} = \frac{{2\cos 4x}}{{2\sin 2x\cos 2x}}\\  \Leftrightarrow \frac{{\cos \left( {2x - x} \right)}}{{\cos x}} = \frac{{\cos 4x}}{{\cos 2x}}\\  \Leftrightarrow \cos 4x = \cos 2x\\  \Leftrightarrow 4x =  \pm 2x + k2\pi \\  \Leftrightarrow \left[ \begin{array}{l} x = k\pi \\ x = k\frac{\pi }{3} \end{array} \right. \Leftrightarrow x = k\frac{\pi }{3} \end{array}$

Để là nghiệm, các giá trị này còn phải thỏa mãn điều kiện sin4x ≠ 0.

Ta có:

- Nếu k chia hết cho 3, tức là k = 3m (m ∈ Z) thì:

- Nếu k không chia hết cho 3, tức là k = 3m±1 (m ∈ Z) thì:

$\sin 4x = \sin \left( { \pm \frac{{4\pi }}{3} + 4m\pi } \right) =  \pm \sin \frac{\pi }{3} =  \pm \frac{{\sqrt 3 }}{2} \ne 0$

Vậy nghiệm của phương trình là $x = k\frac{\pi }{3}$ với k nguyên và không chia hết cho 3.

 

Trên đây là nội dung chi tiết Giải bài tập nâng cao Toán 11 Chương 1 Bài 3 Một số dạng phương trình lượng giác đơn giản với hướng dẫn giải chi tiết, rõ ràng, trình bày khoa học. Hoc247 hy vọng đây sẽ là tài liệu hữu ích giúp các bạn học sinh lớp 11 học tập thật tốt.