Đề thi HK1 môn Toán 10 CTST năm 2023 - 2024 có đáp án trường THPT Phan Chu Trinh

Sở GD & ĐT Đà Nẵng Trường THPT Phan Chu Trinh

Đề kiểm tra Học kì 1 Năm học: 2023 – 2024 Môn: Toán 10 – Chân trời sáng tạo Thời gian: 90p (Không kể thời gian phát đề)

I. PHẦN TRẮC NGHIỆM (7.0 điểm).

Câu 1. Câu nào sau đây không là mệnh đề?

A.  Tam giác đều là tam giác có ba góc bằng nhau.

B. 3 < 1.

C. 4 - 5 = 1.                                                              

D. Bạn học giỏi quá!

Câu 2. Hãy liệt kê các phần tử của tập \(X=\left\{ x\in \mathbb{R}\left| 2{{x}^{2}}-5x+3=0 \right. \right\}\).

A. \(X=\left\{ 0 \right\}\).                                         

B. \(X=\left\{ 1 \right\}\).

C. \(X=\left\{ \frac{3}{2} \right\}\).             

D. \(X=\left\{ 1;\frac{3}{2} \right\}\). 

Câu 3. Cho các tập hợp \(M=\left[ -3;\,6 \right]\) và \(N=\left( -\infty ;\,-2 \right)\cup \left( 3;\,+\infty  \right)\). Khi đó \(M\cap N\) là

A. \(\left( -\infty ;\,-2 \right)\cup \left[ 3;\,6 \right].\)                                         

B. \(\left( -\infty ;\,-2 \right)\cup \left[ 3;\,+\infty  \right)\)

C. \(\left[ -3;\,-2 \right)\cup \left( 3;\,6 \right].\)                                         

D. \(\left( -3;-2 \right)\cup \left( 3;\,6 \right).\) 

Câu 4. Miền nghiệm của bất phương trình \(x+y\le 2\) là phần không bị gạch trong hình vẽ nào?

A.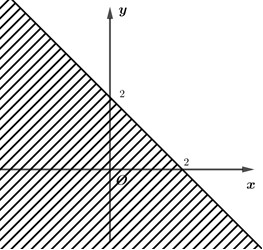

B.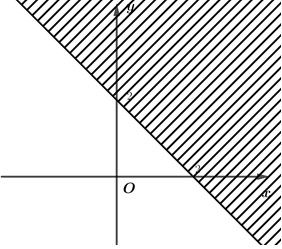

C.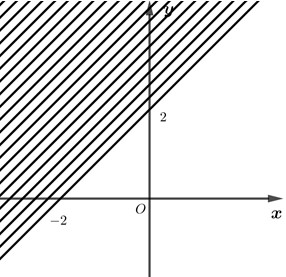

D.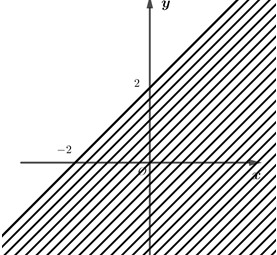

Câu 5. Cho hệ bất phương trình \(\left\{ \begin{align} & x+3y-2\ge 0 \\ & 2x+y+1\le 0 \\ \end{align} \right..\) Trong các điểm sau, điểm nào thuộc miền nghiệm của hệ bất phương trình?

A. \(M\left( 0;1 \right)\).                                         

B. \(N\left( 1;1 \right)\).      

C. \(P\left( 1;3 \right)\).  

D. \(Q\left( 1;0 \right)\). 

Câu 6. Trong các đẳng thức sau, đẳng thức nào đúng?

A. \(\sin \left( {{180}^{\text{O}}}-\alpha  \right)=-\cos \alpha\).                

B. \(\sin \left( {{180}^{\text{O}}}-\alpha  \right)=-\sin \alpha\).                                     

C. \(\sin \left( {{180}^{\text{O}}}-\alpha  \right)=\sin \alpha\).                  

D. \(\sin \left( {{180}^{\text{O}}}-\alpha  \right)=\cos \alpha\). 

Câu 7. Cho \(0<\alpha <\frac{\pi }{2}, ~\cos \alpha =\frac{1}{3}\). Tính \(\sin \alpha\).

A. \(\frac{2\sqrt{2}}{3}\).                           B. \(\frac{2}{3}\).               

C. \(\frac{-2\sqrt{2}}{3}\).                          D. \(\frac{8}{9}\). 

Câu 8. Tìm khẳng định sai trong các khẳng định sau?

A. \({{\left( \sin \alpha +\cos \alpha  \right)}^{2}}=1+2\sin \alpha \cos \alpha\).

B. \({{\left( \sin \alpha -\cos \alpha  \right)}^{2}}=1-2\sin \alpha \cos \alpha\).

C. \({{\cos }^{4}}\alpha -{{\sin }^{4}}\alpha ={{\cos }^{2}}\alpha -{{\sin }^{2}}\alpha\).      

D. \({{\cos }^{4}}\alpha +{{\sin }^{4}}\alpha =1\). 

Câu 9. Cho \(\Delta ABC\) có \(AC=6,AB=8,\widehat{A}={{60}^{0}}\). Độ dài cạnh a bằng

A. \(2\sqrt{13}\).                 B. \(3\sqrt{12}\).            

C. \(2\sqrt{37}\).                 D. \(\sqrt{20}\).    

Câu 10. Mệnh đề nào sau đây đúng?

A. Có duy nhất một vectơ cùng phương với mọi vectơ.

B. Có ít nhất hai vectơ có cùng phương với mọi vectơ.

C. Có vô số vectơ cùng phương với mọi vectơ.

D. Không có vectơ nào cùng phương với mọi vectơ.

Câu 11. Gọi M, N lần lượt là trung điểm của các cạnh AB, AC của tam giác đều ABC. Hỏi cặp vectơ nào sau đây cùng hướng?

A. \(\overrightarrow{MN}\) và \(\overrightarrow{CB}\).                                         

B. \(\overrightarrow{AB}\) và \(\overrightarrow{MB}\). 

C. \(\overrightarrow{MA}\) và \(\overrightarrow{MB}\).                         

D. \(\overrightarrow{AN}\) và \(\overrightarrow{CA}\).

Câu 12. Cho ba điểm phân biệt A, B, C. Đẳng thức nào sau đây đúng?

A. \(\overrightarrow{CA}-\overrightarrow{BA}=\overrightarrow{BC}\).  

B. \(\overrightarrow{AB}+\overrightarrow{AC}=\overrightarrow{BC}\).      

C. \(\overrightarrow{AB}+\overrightarrow{CA}=\overrightarrow{CB}\).      

D. \(\overrightarrow{AB}-\overrightarrow{BC}=\overrightarrow{CA}\). 

Câu 13. Cho tam giác ABC đều cạnh a. Tính \(\left| \overrightarrow{AB}+\overrightarrow{AC} \right|\).

A. \(\left| \overrightarrow{AB}+\overrightarrow{AC} \right|=a\sqrt{3}\).         

B. \(\left| \overrightarrow{AB}+\overrightarrow{AC} \right|=\frac{a\sqrt{3}}{2}\).

C. \(\left| \overrightarrow{AB}+\overrightarrow{AC} \right|=2a\).                    

D. \(\left| \overrightarrow{AB}+\overrightarrow{AC} \right|=2a\sqrt{3}\). 

Câu 14. Cho tam giác ABC và điểm M thỏa mãn \(\overrightarrow{MB}+\overrightarrow{MC}=\overrightarrow{AB}\). Tìm vị trí điểm M.

A. M là trung điểm của AC.                              

B. M là trung điểm của AB.

C. M là trung điểm của BC.

D. M là điểm thứ tư của hình bình hành ABCM.  

Câu 15. Gọi G  là trọng tâm tam giác ABC. Khẳng định nào sau đây đúng ?

A. \(\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=0\).    

B. \(\overrightarrow{GA}+\overrightarrow{GC}=2\overrightarrow{GB}\).    

C. \(\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{0}\).        

D. \(\overrightarrow{GA}=\overrightarrow{GB}=\overrightarrow{GC}\). 

Câu 16. Cho tam giác \(ABC\). Gọi \(M\) và \(N\) lần lượt là trung điểm của \(AB\) và \(AC.\) Khẳng định nào sau đây sai ?

A. \(\overrightarrow{AB}=2\overrightarrow{AM}.\)                              

B. \(\overrightarrow{AC}=2\overrightarrow{NC}.\)                                    

C. \(\overrightarrow{BC}=-\,2\overrightarrow{MN}.\)                                

D. \(\overrightarrow{CN}=-\frac{1}{2}\overrightarrow{AC}.\) 

Câu 17. Trên đường thẳng MN  lấy điểm P  sao cho \(\overrightarrow{MP}=3\overrightarrow{PN}\). Điểm P được xác định đúng trong hình vẽ nào sau đây.

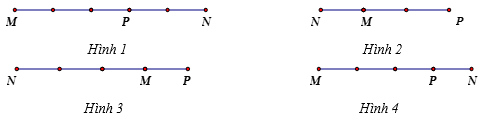
A. Hình 1.                       B. Hình 2.                   C. Hình 3.                       D. Hình 4.

Câu 18. Cho tam giác \(ABC\) có \(M\) là trung điểm của \(BC,\,\,\,G\) là trọng tâm của tam giác\(ABC.\) Khẳng định nào sau đây đúng ?

A. \(\overrightarrow{AG}=\frac{2}{3}\overrightarrow{AM}.\)                  

B. \(\overrightarrow{AG}=\frac{3}{2}\overrightarrow{AM}.\)                       

C. \(\overrightarrow{AG}=-\frac{2}{3}\overrightarrow{AM}.\)                    

D. \(\overrightarrow{AG}=-\frac{3}{2}\overrightarrow{AM}.\) 

Câu 19. Trong mặt phẳng tọa độ Oxy, cho \(\vec{u}=-2\vec{i}+\vec{j}\). Tìm tọa độ của vectơ \(\vec{u}\).

A. \(\vec{u}\left( 2;-1 \right).\)                                  

B. \(\vec{u}\left( -2;1 \right).\) 

C. \(\vec{u}\left( 2;1 \right).\)               

D. \(\vec{u}\left( -2;-1 \right).\) 

Câu 20. Trong mặt phẳng tọa độ Oxy, cặp vectơ nào sau đây cùng phương?

A. \(\vec{a}\left( 1;0 \right)và \vec{b}\left( 0;1 \right).\)                                      

B. \(\vec{a}\left( 3;-2 \right)và \vec{b}\left( 6;4 \right).\)

C. \(\vec{a}\left( 2;3 \right)và \vec{b}\left( -6;-9 \right).\)        

D. \(\vec{a}\left( 2;3 \right)và \vec{b}\left( -6;9 \right).\)

---(Để xem tiếp nội dung trắc nghiệm của đề thi các em vui lòng xem tại online hoặc đăng nhập vào HỌC247 để tải về máy)---

1. D	2. D	3. C	4. B	5. B	6. C	7. A	8. D	9. A	10. A
11. B	12. C	13. A	14. A	15. C	16. C	17. D	18. A	19. B	20. C
21. D	22. B	23. A	24. D	25. C	26. C	27. B	28. C	29. B	30. A
31. B	32. B	33. B	34. A	35. A

Trên đây là một phần trích đoạn nội dung Đề thi HK1 môn Toán 10 CTST năm 2023 - 2024 có đáp án trường THPT Phan Chu Trinh. Để xem toàn bộ nội dung các em chọn chức năng xem online hoặc đăng nhập vào trang hoc247.net để tải tài liệu về máy tính.

Mời các em tham khảo tài liệu có liên quan:

• Đề thi HK1 môn Vật lí 10 KNTT năm 2023-2024 có đáp án trường THPT Nguyễn Cao Thắng

• Bộ 3 đề thi HK1 môn Vật lí 10 CTST năm 2023-2024 có đáp án trường THPT Trịnh Hoài Đức

Hy vọng bộ đề thi này sẽ giúp các em học sinh ôn tập tốt và đạt thành tích cao trong kì thi sắp tới.