Vß╗øi mong muß╗æn c├│ th├¬m t├Āi liß╗ću cung cß║źp gi├║p c├Īc em hß╗Źc sinh lß╗øp 10 ├┤n tß║Łp r├©n luyß╗ćn chuß║®n bß╗ŗ cho k├¼ thi giß╗»a HK1 sß║»p tß╗øi. HOC247 giß╗øi thiß╗ću ─æß║┐n c├Īc em t├Āi liß╗ću ─Éß╗ü thi giß╗»a HK1 m├┤n To├Īn 10 C├Īnh diß╗üu n─ām 2022-2023 c├│ ─æ├Īp ├Īn TrŲ░ß╗Øng THPT Ng├┤ Quyß╗ün. Hi vß╗Źng ─æ├óy l├Ā t├Āi liß╗ću hß╗»u ├Łch cho c├Īc em trong qu├Ī tr├¼nh hß╗Źc tß║Łp v├Ā ├┤n thi To├Īn 10 C├Īnh diß╗üu.
|
TRŲ»ß╗£NG THPT NG├ö QUYß╗ĆN |
─Éß╗Ć THI GIß╗«A Hß╗īC K├ī 1 M├öN TO├üN 10 C├üNH DIß╗ĆU N─éM Hß╗īC 2022 ŌĆō 2023 Thß╗Øi gian: 90 ph├║t |
I. PHß║”N TRß║«C NGHIß╗åM
C├óu 1. Cho t├ó╠Żp hŲĪ╠Żp A va╠Ć a la╠Ć m├┤╠Żt ph├ó╠Ćn tŲ░╠ē cu╠ēa t├ó╠Żp hß╗Żp A. Trong c├Īc mß╗ćnh ─æß╗ü sau, mß╗ćnh ─æß╗ü n├Āo sai?
A. {a} ŌŖé A;
B. {a} Ōłł A;
C. a Ōłł A;
D. ŌłģŌŖéA.
C├óu 2. Cho m├¬╠Żnh ─æ├¬╠Ć chŲ░╠üa bi├¬╠ün P(n): chia hß║┐t cho 4 ŌĆØ vŲĪ╠üi n la╠Ć s├┤╠ü nguy├¬n. Cho╠Żn m├¬╠Żnh ─æ├¬╠Ć ─æu╠üng trong ca╠üc m├¬╠Żnh ─æ├¬╠Ć sau:
A. P(5);
B. P(2);
C. P(4);
D. P(6).
C├óu 3.Mß╗ćnh ─æß╗ü phß╗¦ ─æß╗ŗnh cß╗¦a mß╗ćnh ─æß╗ü ŌĆ£PhŲ░ŲĪng tr├¼nh ax2 + bx + c = 0 (a ŌēĀ 0) v├┤ nghiß╗ćmŌĆØ l├Ā:
A. PhŲ░ŲĪng tr├¼nh ax2 + bx + c = 0 (a ŌēĀ 0) kh├┤ng c├│ nghiß╗ćm;
B. PhŲ░ŲĪng tr├¼nh ax2 + bx + c = 0 (a ŌēĀ 0) c├│ nghiß╗ćm;
C. PhŲ░ŲĪng tr├¼nh ax2 + bx + c = 0 (a ŌēĀ 0) c├│ 2 nghiß╗ćm ph├ón biß╗ćt;
D. PhŲ░ŲĪng tr├¼nh ax2 + bx + c = 0 (a ŌēĀ 0) c├│ nghiß╗ćm k├®p.
C├óu 4. Go╠Żi A la╠Ć t├ó╠Żp hŲĪ╠Żp ca╠üc s├┤╠ü thŲ░╠Żc kh├┤ng nho╠ē hŲĪn 1 va╠Ć B la╠Ć t├ó╠Żp hŲĪ╠Żp ca╠üc s├┤╠ü thŲ░╠Żc co╠ü gia╠ü tri╠Ż tuy├¬╠Żt ─æ├┤╠üi nho╠ē hŲĪn 2. Ti╠Ćm AŌł®B
A. AŌł®B=(1;2)
B. AŌł®B=[1;2)
C. AŌł®B=[1;2]
D. AŌł®B=(ŌłÆ2;1)
C├óu 5. Cho A = {0; 1; 2; 3; 4} v├Ā B = {2; 3; 4; 5; 6}. Tß║Łp hß╗Żp (A \ B) Ōł¬ (B \ A) bß║▒ng?
A. {5; 6};
B. {2; 3; 4};
C. {1; 2};
D. {0; 1; 5; 6}.
C├óu 6: Sß╗æ phß║¦n tß╗Ł cß╗¦a tß║Łp hß╗Żp A = {k2 + 1| k Ōłł Ōäż, |k| Ōēż 2} bß║▒ng
A. 1;
B. 5;
C. 3;
D. 2.
C├óu 7: Cho hai tß║Łp hß╗Żp (1; 3) v├Ā [2; 4]. Giao cß╗¦a hai tß║Łp hß╗Żp ─æ├Ż cho l├Ā
A. (2; 3];
B. (2; 3);
C. [2; 3);
D. [2; 3].
C├óu 8: H├¼nh vß║Į sau ─æ├óy (phß║¦n kh├┤ng bß╗ŗ gß║Īch) l├Ā biß╗āu diß╗ģn cß╗¦a tß║Łp hß╗Żp n├Āo?
A. (ŌĆō Ōł×; ŌĆō 2) Ōł¬ [5; +Ōł×);
B. (ŌĆō Ōł×; ŌĆō 2) Ōł¬ (5; +Ōł×);
C. (ŌĆō Ōł×; ŌĆō 2] Ōł¬ (5; +Ōł×);
D. (ŌĆō Ōł×; ŌĆō 2] Ōł¬ [5; +Ōł×).
C├óu 9. Lß╗øp 10A1 c├│ 6 hß╗Źc sinh giß╗Åi To├Īn, 4 hß╗Źc sinh giß╗Åi L├Į, 5 hß╗Źc sinh giß╗Åi H├│a, 2 hß╗Źc sinh giß╗Åi To├Īn v├Ā L├Į, 3 hß╗Źc sinh giß╗Åi To├Īn v├Ā H├│a, 2 hß╗Źc sinh giß╗Åi L├Į v├Ā H├│a, 1 hß╗Źc sinh giß╗Åi cß║Ż 3 m├┤n To├Īn, L├Į, H├│a. Sß╗æ hß╗Źc sinh giß╗Åi ├Łt nhß║źt mß╗Öt m├┤n (To├Īn, L├Į, H├│a) cß╗¦a lß╗øp 10A1 l├Ā:
A. 15;
B. 23;
C. 7;
D. 9.
C├óu 10. Cß║Ęp sß╗æ (x; y) n├Āo sau ─æ├óy l├Ā nghiß╗ćm cß╗¦a bß║źt phŲ░ŲĪng tr├¼nh 5x ŌĆō 3y Ōēż 2?
A. (0; ŌĆō 2);
B. (3; 0);
C. (2; 1);
D. (ŌĆō 1; ŌĆō 1).
C├óu 11. Bß║źt phŲ░ŲĪng tr├¼nh n├Āo sau ─æ├óy kh├┤ng l├Ā bß║źt phŲ░ŲĪng tr├¼nh bß║Łc nhß║źt mß╗Öt ß║®n?
A. 8 ŌĆō \(\sqrt{2}\)x Ōēż 0;
B. 4x ŌĆō 3 > 0;
C. \(\frac{1}{3}\)x ŌĆō 3 < 0;
D. (x + 1)2 Ōēź 1.
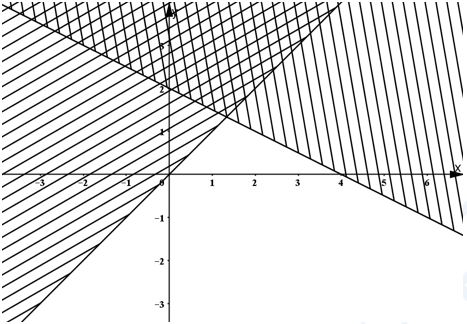
C├óu 12. Phß║¦n mß║Ęt phß║│ng kh├┤ng bß╗ŗ gß║Īch ch├®o trong h├¼nh vß║Į b├¬n (kß╗ā cß║Ż bi├¬n) l├Ā biß╗āu diß╗ģn h├¼nh hß╗Źc tß║Łp nghiß╗ćm cß╗¦a hß╗ć bß║źt phŲ░ŲĪng tr├¼nh n├Āo dŲ░ß╗øi ─æ├óy?
A \(\left\{ {\begin{array}{*{20}{l}}
{x - y \ge 0}\\
{x + 2y \le 4}
\end{array}} \right.\)
B. \(\left\{ {\begin{array}{*{20}{l}}
{x - y \le 0}\\
{x + 2y \ge 4}
\end{array}} \right.\)
C. \(\left\{ {\begin{array}{*{20}{l}}
{x - y \ge 0}\\
{x + 2y \ge 4}
\end{array}} \right.\)
D. \(\left\{ {\begin{array}{*{20}{l}}
{x - y \le 0}\\
{x + 2y \le 4}
\end{array}} \right.\)
C├óu 13. Cho sin35┬░ Ōēł 0,57. Gi├Ī trß╗ŗ cß╗¦a sin145┬░ gß║¦n vß╗øi gi├Ī trß╗ŗ n├Āo nhß║źt sau ─æ├óy:
A. 0,57;
B. 1;
C. \(\frac{\sqrt{2}}{2}\);
D. 0,15.
C├óu 14. T├Łnh gi├Ī trß╗ŗ biß╗āu thß╗®c: A = cos 0┬░ + cos 40┬░ + cos 120┬░ + cos 140┬░
A. \(\frac{1}{2}\);
B. ŌĆō 0,5;
C. 1;
D. 0.
C├óu 15. Cho tam gi├Īc ABC, ta c├│ c├Īc ─æß║│ng thß╗®c:
(I) \(sin\frac{A}{2}=\sin \frac{B+C}{2}\);
(II) \(\tan \frac{A}{2}=\cot \frac{B+C}{2}\);
(III) sinA = sin(B + C).
C├│ bao nhi├¬u ─æß║│ng thß╗®c ─æ├║ng?
A. 1
B. 3
C. 2
D. 0.
C├óu 16. Cho ─æiß╗ām M(x0; y0) nß║▒m tr├¬n ─æŲ░ß╗Øng tr├▓n ─æŲĪn vß╗ŗ thß╗Åa m├Żn \(\widehat{xOM}=\alpha \). Khi ─æ├│ ph├Īt biß╗āu n├Āo dŲ░ß╗øi ─æ├óy l├Ā sai?
A. sin╬▒ = x0;
B. cos╬▒ = x0;
C. tan╬▒ = \(\frac{{{y}_{0}}}{{{x}_{0}}}\);
D. cot╬▒ = \(\frac{{{x}_{0}}}{{{y}_{0}}}\).
C├óu 17. Trong c├Īc c├┤ng thß╗®c dŲ░ß╗øi ─æ├óy, c├┤ng thß╗®c n├Āo sai vß╗ü c├Īch t├Łnh diß╗ćn t├Łch tam gi├Īc ABC? Biß║┐t AB = c, AC = b, BC = a, ha, hb, hc lß║¦n lŲ░ß╗Żt l├Ā c├Īc ─æŲ░ß╗Øng cao kß║╗ tß╗½ ─æß╗ēnh A, B, C, r l├Ā b├Īn k├Łnh ─æŲ░ß╗Øng tr├▓n nß╗Öi tiß║┐p, R l├Ā b├Īn k├Łnh ─æŲ░ß╗Øng tr├▓n ngoß║Īi tiß║┐p tam gi├Īc ABC.
A. SABC = pr;
B. SABC = \(\frac{1}{2}\).c.a.sinA;
C. SABC = \(\sqrt{p\left( p-a \right)\left( p-b \right)\left( p-c \right)}\);
D. SABC = \(\frac{abc}{4R}\).
C├óu 18. Cho tam gi├Īc ABC, c├│ c├Īc cß║Īnh AB = c, AC = b, BC = a. ─Éß╗ŗnh l├Ł sin ─æŲ░ß╗Żc ph├Īt biß╗āu:
A. \(\frac{a}{\text{cos}A}=\frac{b}{\cos B}=\frac{c}{\cos C}\)
B. \(\frac{a}{\text{sin}A}=\frac{b}{\sin B}=\frac{c}{\sin C}\)
C. a.cosA = b.cosB = c.cosC;
D. a.sinA = b.sinB = c.sinC.
C├óu 19. Cho tam gi├Īc ABC c├│ BC = 50 cm, \(\hat{B}=65{}^\circ ,\hat{C}=45{}^\circ \). T├Łnh (l├Ām tr├▓n kß║┐t quß║Ż ─æß║┐n h├Āng phß║¦n mŲ░ß╗Øi theo ─æŲĪn vß╗ŗ x─āng ŌĆō ti ŌĆō m├®t). Chu vi cß╗¦a tam gi├Īc ABC l├Ā:
A. 135,84;
B. 67,92;
C. 131,91;
D. 65,96.
C├óu 20. Mß╗Öt ngŲ░ß╗Øi ─æß╗®ng ß╗¤ vß╗ŗ tr├Ł A tr├¬n n├│c mß╗Öt ng├┤i nh├Ā cao 8m ─æang quan s├Īt mß╗Öt c├óy cao c├Īch ng├┤i nh├Ā 25m v├Ā ─æo ─æŲ░ß╗Żc \(\widehat{BAC}=65{}^\circ \). Chiß╗üu cao cß╗¦a c├óy gß║¦n vß╗øi kß║┐t quß║Ż n├Āo nhß║źt sau ─æ├óy?
A. 38m;
B. 39m;
C. 19m;
D. 20m.
....................
---(─Éß╗ā xem tiß║┐p nß╗Öi dung cß╗¦a ─æß╗ü thi c├Īc em vui l├▓ng xem tß║Īi online hoß║Ęc ─æ─āng nhß║Łp v├Āo Hß╗īC247 ─æß╗ā tß║Żi vß╗ü m├Īy)---
Tr├¬n ─æ├óy l├Ā mß╗Öt phß║¦n nß╗Öi dung t├Āi liß╗ću ─Éß╗ü thi giß╗»a HK1 m├┤n To├Īn 10 C├Īnh diß╗üu n─ām 2022-2023 c├│ ─æ├Īp ├Īn TrŲ░ß╗Øng THPT Ng├┤ Quyß╗ün. ─Éß╗ā xem th├¬m nhiß╗üu t├Āi liß╗ću tham khß║Żo hß╗»u ├Łch kh├Īc c├Īc em chß╗Źn chß╗®c n─āng xem online hoß║Ęc ─æ─āng nhß║Łp v├Āo trang hoc247.net ─æß╗ā tß║Żi t├Āi liß╗ću vß╗ü m├Īy t├Łnh.
Mß╗Øi c├Īc em tham khß║Żo t├Āi liß╗ću c├│ li├¬n quan:
- ─Éß╗ü thi giß╗»a HK1 m├┤n To├Īn 10 KNTT n─ām 2022-2023 c├│ ─æ├Īp ├Īn TrŲ░ß╗Øng THPT TrŲ░ng VŲ░ŲĪng
- ─Éß╗ü thi giß╗»a HK1 m├┤n To├Īn 10 CTST n─ām 2022-2023 c├│ ─æ├Īp ├Īn TrŲ░ß╗Øng THPT Quang Trung
Hy vß╗Źng t├Āi liß╗ću n├Āy sß║Į gi├║p c├Īc em hß╗Źc sinh ├┤n tß║Łp tß╗æt v├Ā ─æß║Īt th├Ānh t├Łch cao trong k├¼ thi sß║»p tß╗øi.


.JPG?enablejsapi=1)