Bài tập 6.3 trang 106 SBT Toán 9 Tập 2

Hướng dẫn giải

Ta sử dụng kiến thức:

+) Trong tam giác đều, mỗi góc đều bằng $60^\circ.$

+) Chứng minh ba điểm thẳng hàng: Nếu $\widehat{ABD}+\widehat{DBC}=180^\circ$ thì $A,B,C$ thẳng hàng.

Lời giải chi tiết

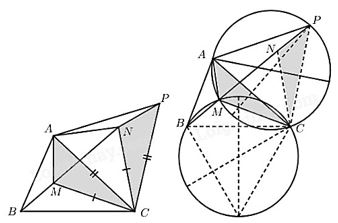
Trong $∆ABC$ ta lấy điểm $M.$ Nối $MA, MB, MC.$

Ta cần làm xuất hiện tổng $MA + MB + MC$ sau đó tìm điều kiện để tổng đó nhỏ nhất.

Lấy $MC$ làm cạnh dựng trên nửa mặt phẳng bờ $BC$ chứa điểm $A$ tam giác đều $MCN.$ Suy ra: $CM = MN.$

Lấy $AC$ làm cạnh dựng trên nửa mặt phẳng bờ $AC$ không chứa điểm $B$ tam giác đều $APC.$

Ta có:

$\widehat {MCA} + \widehat {ACN} = \widehat {MCN}=60^\circ$

$\widehat {ACN} + \widehat {NCP} =\widehat {ACP}= 60^\circ$

$\Rightarrow \widehat {MCA} = \widehat {NCP}$ 

Xét $∆AMC$ và $∆PNC:$

+) $CM = CN$ (vì $∆MCN$ đều)

+) $\widehat {MCA} = \widehat {NCP}$ (chứng minh trên)

+) $CA = CP$ (vì $∆APC$ đều)

Suy ra: $∆AMC = ∆PNC\;\; (c.g.c)$

$\Rightarrow         PN = AM$

$MA + MB + MC = NP + MB + MN$

Ta có $∆ABC$ cho trước nên điểm $P$ cố định nên $BM + MN + NP$ ngắn nhất khi $4$ điểm $B, M, N, P$ thẳng hàng.

Vì $\widehat {CMN} = 60^\circ$ nên $3$ điểm $B, M, N$ thẳng hàng khi và chỉ khi $\widehat {BMC} = 120^\circ$

Vì $\widehat {CNM} = 60^\circ$ nên $3$ điểm $M, N, P$ thẳng hàng khi và chỉ khi $\widehat {CNP} = 120^\circ$

Mà $∆AMC = ∆PNC$ (chứng minh trên)     $\Rightarrow \widehat {AMC} = \widehat {PNC} = 120^\circ$

Vậy $MA + MB + MC$ bé nhất khi và chỉ khi $\widehat {BMC} = 120^\circ$  và $\widehat {AMC} = 120^\circ$

Vậy $M$ là giao điểm của $2$ cung chứa góc $120^\circ$ dựng trên $BC$  và $AC.$

-- Mod Toán 9 HỌC247