Bài tập 31 trang 90 SBT Toán 8 Tập 2

Hướng dẫn giải

Sử dụng:

- Nếu ba cạnh của tam giác này tỉ lệ với ba cạnh của tam giác kia thì hai tam giác đó đồng dạng.

- Tính chất: Đường trung bình tam giác thì song song với cạnh thứ ba và bằng nửa cạnh ấy.

Lời giải chi tiết

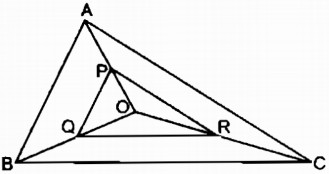
Xét \( ∆ OAB\) có \(PQ\) là đường trung bình nên \(\displaystyle PQ = {1 \over 2}AB\) (tính chất đường trung bình của tam giác).

\( \Rightarrow \displaystyle {{PQ} \over {AB}} = {1 \over 2}\)        (1)

Xét \(∆ OAC\) có \(PR\) là đường trung bình nên \(\displaystyle  PR = {1 \over 2}AC\) (tính chất đường trung bình của tam giác)

\( \Rightarrow \displaystyle {{PR} \over {AC}} = {1 \over 2}\)         (2)

Xét \(∆ OBC\) có \(QR\) là đường trung bình nên \(\displaystyle QR = {1 \over 2}BC\) (tính chất đường trung bình của tam giác )

\( \Rightarrow \displaystyle{{QR} \over {BC}} = {1 \over 2}\)          (3)

Từ (1), (2) và (3) suy ra: \(\displaystyle {{PQ} \over {AB}} = {{PR} \over {AC}} = {{QR} \over {BC}}= {1 \over 2}\)

Vậy \(∆ PQR\) đồng dạng \(∆ ABC\) (c.c.c).

-- Mod Toán 8 HỌC247