Giải bài 33 tr 91 sách BT Toán lớp 8 Tập 2
Cho tam giác ABC và một điểm O nằm trong tam giác đó. Gọi P, Q, R lần lượt là trung điểm của các đoạn thẳng OA, OB, OC.
a. Chứng minh rằng tam giác PQR đồng dạng với tam giác ABC.
b. Tính chu vi của tam giác PQR, biết rằng tam giác ABC có chu vi p bằng 543cm.
Hướng dẫn giải chi tiết
Hướng dẫn giải
Sử dụng:
- Nếu ba cạnh của tam giác này tỉ lệ với ba cạnh của tam giác kia thì hai tam giác đó đồng dạng.
- Tính chất: Đường trung bình tam giác thì song song với cạnh thứ ba và bằng nửa cạnh ấy.
- Tính chất của dãy tỉ số bằng nhau: \(\dfrac{a}{b} = \dfrac{c}{d} = \dfrac{e}{f} = \dfrac{{a + c + e}}{{b + d + f}}\)
Lời giải chi tiết
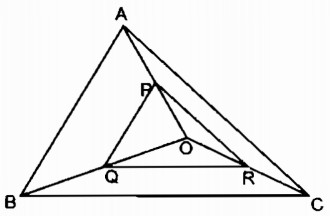
a. Trong tam giác AOB, ta có:
P trung điểm của OA (gt)
Q trung điểm của OB (gt)
Suy ra: PQ là đường trung bình của ∆ OAB.
Suy ra: \(PQ = {1 \over 2}AB\)
(tính chất đường trung bình của tam giác )
Suy ra: \({{PQ} \over {AB}} = {1 \over 2}\) (1)
Trong tam giác OAC, ta có:
P trung điểm của OA (gt)
R trung điểm của OC (gt)
Suy ra: PR là đường trung bình của tam giác OAC.
Suy ra: \(PR = {1 \over 2}AC\) (tính chất đường trung bình của tam giác )
Suy ra: \({{PR} \over {AC}} = {1 \over 2}\) (2)
Trong tam giác OBC, ta có:
Q trung điểm của OB (gt)
R trung điểm của OC (gt)
Suy ra: QR là đường trung bình của tam giác OBC.
Suy ra: \(QR = {1 \over 2}BC\) (tính chất đường trung bình của tam giác )
Suy ra: \({{QR} \over {BC}} = {1 \over 2}\) (3)
Từ (1), (2) và (3) suy ra: \({{PQ} \over {AB}} = {{PR} \over {AC}} = {{QR} \over {BC}} = {1 \over 2}\)
Vậy ∆ PQR đồng dạng ∆ ABC (c.c.c)
b. Gọi p’ là chu vi tam giác PQR.
Ta có: \({{PQ} \over {AB}} = {{PR} \over {AC}} = {{QR} \over {BC}} = {{PQ + PR + QR} \over {AB + AC + BC}} = {{p'} \over p}\)
Vậy: \({{p'} \over p} = {1 \over 2} \Rightarrow p' = {1 \over 2}p = {1 \over 2}.543 = 271,5\) (cm)
-- Mod Toán 8 HỌC247
-


Bài 34 trang 91 sách bài tập tập 2 toán 8
bởi thanh hằng
 31/05/2019
Bài 34 (Sách bài tập - tập 2 - trang 91)
31/05/2019
Bài 34 (Sách bài tập - tập 2 - trang 91)Cho trước tam giác ABC. Hãy dựng một tam giác đồng dạng với tam giác ABC theo tỉ số \(k=\dfrac{2}{3}\)
Theo dõi (0) 1 Trả lời -


Bài 33 trang 91 sách bài tập tập 2 toán 8
bởi Sam sung
 31/05/2019
Bài 33 (Sách bài tập - tập 2 - trang 91)
31/05/2019
Bài 33 (Sách bài tập - tập 2 - trang 91)Cho tam giác ABC và một điểm O nằm trong tam giác đó. Gọi P, Q, R lần lượt là trung điểm của các đoạn thẳng OA, OB, OC
a) Chứng minh rằng tam giác PQR đồng dạng với tam giác ABC
b) Tính chu vi của tam giác PQR, biết rằng tam giác ABC có chu vi p bằng 543 cm
Theo dõi (0) 1 Trả lời -


Bài 31 trang 90 sách bài tập toán 8 tập 2
bởi Trịnh Lan Trinh
 31/05/2019
Bài 31 (Sách bài tập - tập 2 - trang 90)
31/05/2019
Bài 31 (Sách bài tập - tập 2 - trang 90)Tam giác ABC có ba đường trung tuyến cắt nhau tại O. Gọi P, Q, R thứ tự là trung điểm của các đoạn thẳng OA, OB, OC
Chứng minh rằng tam giác PQR đồng dạng với tam giác ABC ?
Theo dõi (0) 1 Trả lời





