Luyện tập 4 trang 59 SGK Toán 7 Cánh diều tập 2 - CD

Phương pháp giải

Nhớ lại cách thức trừ hai đa thức theo cột dọc và theo hàng ngang:

Để trừ đa thức P(x) cho đa thức Q(x) (theo cột dọc), ta có thể làm như sau:

- Thu gọn mỗi đa thức và sắp xếp hai đa thức đó cùng theo số mũ giảm dần (hoặc tăng dần) của biến;

- Đặt hai đơn thức có cùng số mũ của biến ở cùng cột sao cho đơn thức P(x) ở trên và đơn thức của Q(x) ở dưới;

- Trừ hai đơn thức trong từng cột, ta có hiệu cần tìm.

Để trừ đa thức P(x) cho đa thức Q(x) (theo hàng ngang), ta có thể làm như sau:

- Thu gọn mỗi đa thức và sắp xếp hai đa thức đó cùng theo số mũ giảm dần (hoặc tăng dần) của biến;

- Viết hiệu P(x) – Q(x) theo hàng ngang, trong đó đa thức Q(x) được đặt trong dấu ngoặc;

- Sau khi bỏ dấu ngoặc và đổi dấu mỗi đơn thức trong dạng thu gọn của đa thức Q(x), nhóm các đơn thức có cùng số mũ của biến với nhau;

- Thực hiện phép tính trong từng nhóm, ta được hiệu cần tìm.

Lời giải chi tiết

Theo cột dọc:

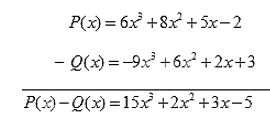
Theo hàng ngang:

\(\begin{array}{l}P(x) - Q(x) = 6{x^3} + 8{x^2} + 5x - 2 - ( - 9{x^3} + 6{x^2} + 2x + 3)\\ = 6{x^3} + 8{x^2} + 5x - 2 + 9{x^3} - 6{x^2} - 2x - 3\\ = (6 + 9){x^3} + (8 - 6){x^2} + (5 - 2)x + ( - 2 - 3)\\ = 15{x^3} + 2{x^2} + 3x - 5\end{array}\)

-- Mod Toán 7 HỌC247