Luyện tập 3 trang 118 SGK Toán 7 Cánh diều tập 2
Cho tam giác ABC có trực tâm H cũng là trọng tâm của tam giác. Chứng minh tam giác ABC đều.
Hướng dẫn giải chi tiết Luyện tập 3
Phương pháp giải
Chứng minh AB = AC = BC
Lời giải chi tiết
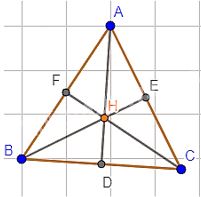
Giả sử tam giác ABC có H vừa là trực tâm, vừa là trọng tâm tam giác ABC. Ta phải chứng minh tam giác ABC đều.
Vì H là trọng tâm tam giác ABC nên AD, BE, CF vừa là các đường cao, vừa là các đường trung tuyến trong tam giác.
Suy ra: AF = BF = AE = CE = BD = CD;
\(AD \bot BC; BE \bot AC; CF \bot AB\)
Xét tam giác ADB và tam giác ADC có:
AD chung
\(\widehat{ADB}=\widehat{ADC} (=90^0)\)
BD = CD (D là trung điểm của đoạn thẳng BC).
Vậy \(\Delta ADB = \Delta ADC\)(c.g.c) nên AB = AC ( 2 cạnh tương ứng).
Tương tự, ta cũng được, AC = BC
Xét tam giác ABC có AB = AC = BC nên là tam giác đều.
Vậy tam giác ABC có trực tâm H cũng là trọng tâm của tam giác thì tam giác ABC đều.
-- Mod Toán 7 HỌC247
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.
Bài tập SGK khác
Hoạt động 2 trang 117 SGK Toán 7 Cánh diều tập 2 - CD
Luyện tập 2 trang 117 SGK Toán 7 Cánh diều tập 2 - CD
Giải bài 1 trang 118 SGK Toán 7 Cánh diều tập 2 - CD
Giải bài 2 trang 118 SGK Toán 7 Cánh diều tập 2 - CD
Giải bài 3 trang 118 SGK Toán 7 Cánh diều tập 2 - CD
Giải bài 4 trang 118 SGK Toán 7 Cánh diều tập 2 - CD
Giải bài 5 trang 118 SGK Toán 7 Cánh diều tập 2 - CD
Giải bài 6 trang 118 SGK Toán 7 Cánh diều tập 2 - CD
Giải bài 92 trang 97 SBT Toán 7 Cánh diều tập 2 - CD
Giải bài 93 trang 97 SBT Toán 7 Cánh diều tập 2 - CD
Giải bài 94 trang 97 SBT Toán 7 Cánh diều tập 2 - CD
Giải bài 95 trang 97 SBT Toán 7 Cánh diều tập 2 - CD
Giải bài 96 trang 97 SBT Toán 7 Cánh diều tập 2 - CD