Giải bài 94 trang 97 SBT Toán 7 Cánh diều tập 2
Cho tam giác ABC nhọn có các đường cao AD, BE, CF cắt nhau tại H (Hình 61). Tìm trực tâm của các tam giác HAB, HBC, HCA.
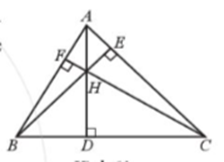
Hướng dẫn giải chi tiết Bài 94
Phương pháp giải
Xác định các đường cao của tam giác HAB, HBC, HCA cắt nhau nhau tại điểm nào thì điểm đó là trực tâm của tam giác.
Lời giải chi tiết
•Xét tam giác HAB có BD ⊥ AH, AE ⊥ BH, HF ⊥ AB và ba đường cao BD, AE, HF cắt nhau tại C.
Do đó C là trực tâm tam giác HAB.
•Xét tam giác HBC có HD ⊥ BC, BF ⊥ HC, CE ⊥ BH và ba đường cao HD, BF, CEcắt nhau tại A.
Do đó A là trực tâm tam giác HBC.
•Xét tam giác HCA có HE ⊥ AC, AF ⊥ HC, CD ⊥ AH và ba đường cao HE, AF, CD cắt nhau tại B.
Do đó B là trực tâm tam giác HCA.
Vậy trực tâm của các tam giác HAB, HBC, HCA tương ứng là C, A, B.
-- Mod Toán 7 HỌC247
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.





