Giải bài 7 trang 77 SGK Toán 7 Cánh diều tập 2
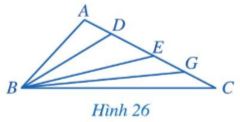
Cho tam giác ABC có góc A tù. Trên cạnh AC lần lượt lấy các điểm D, E, G sao cho D nằm giữa A và E; E nằm giữa D và G; G nằm giữa E và C (Hình 26). Sắp xếp các đoạn thẳng BA, BD, BE, BG, BC theo thứ tự tăng dần. Giải thích vì sao?
Hướng dẫn giải chi tiết Bài 7
Phương pháp giải
Muốn sắp xếp được các đoạn thẳng theo thứ tự tăng dần, ta so sánh chúng với BA và cạnh còn lại trong tam giác tương ứng
Lời giải chi tiết
Xét tam giác BAD:
+ Góc A tù (góc > 90°) nên cạnh BD là cạnh lớn nhất trong tam giác này (đối diện với góc A).
Nên BD > BA.
+ Góc A tù nên góc ABD và góc ADB là góc nhọn → góc BDE là góc tù (ba điểm A, D, E thẳng hàng hay góc ADE =180°). Vậy BE (đối diện với góc BDE) > BD.
Tương tự, ta có:
+ Góc BDE là góc tù nên góc DBE và góc DEB là góc nhọn → góc BEG là góc tù. Vậy BG > BE.
+ Góc BEG là góc tù nên góc EBG và góc EGB là góc nhọn → góc BGC là góc tù. Vậy BC > BG.
Vậy BA < BD <BE < BG < BC.
Hay các đoạn thẳng BA, BD, BE, BG, BC theo thứ tự tăng dần là: BA, BD, BE, BG, BC.
-- Mod Toán 7 HỌC247
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.
Bài tập SGK khác
Giải bài 5 trang 77 SGK Toán 7 Cánh diều tập 2 - CD
Giải bài 6 trang 77 SGK Toán 7 Cánh diều tập 2 - CD
Giải bài 12 trang 70 SBT Toán 7 Cánh diều tập 2 - CD
Giải bài 13 trang 70 SBT Toán 7 Cánh diều tập 2 - CD
Giải bài 14 trang 70 SBT Toán 7 Cánh diều tập 2 - CD
Giải bài 15 trang 71 SBT Toán 7 Cánh diều tập 2 - CD
Giải bài 16 trang 71 SBT Toán 7 Cánh diều tập 2 - CD