Giải bài 17 trang 71 SBT Toán 7 Cánh diều tập 2
Cho tam giác ABC, điểm D nằm giữa hai điểm B và C. Chứng minh AD nhỏ hơn nửa chu vi của tam giác ABC.
Hướng dẫn giải chi tiết Bài 17
Phương pháp giải
Áp dụng bất đẳng thức tam giác trong tam giác ABC để chứng minh \(A{\rm{D}} < \frac{{AB + AC + BC}}{2}\)
Lời giải chi tiết
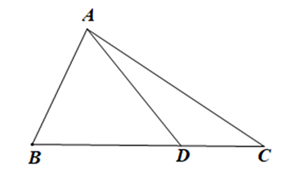
Xét ∆ABD có: AD < AB + BD (bất đẳng thức tam giác) (1)
Xét ∆ACD có AD < AC + DC (bất đẳng thức tam giác) (2)
Cộng theo vế của (1) và (2) ta có:
AD + AD < AB + BD + AC + DC
2AD < AB + AC + (BD + DC)
2AD < AB +AC +BC
Suy ra: \(A{\rm{D}} < \frac{{AB + AC + BC}}{2}\)
Mà\(\frac{{AB + AC + BC}}{2}\) là chu vi của tam giác ABC.
Vậy AD luôn nhỏ hơn nửa chu vi của tam giác ABC.
-- Mod Toán 7 HỌC247
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.





