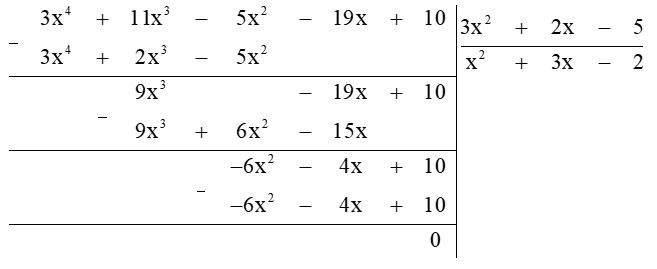Giải bài 7.31 trang 34 SBT Toán 7 Kết nối tri thức tập 2 - KNTT

Phương pháp giải:

\(\begin{array}{l}A\left( x \right) = \left( {3{x^2} + 2x - 5} \right).H\left( x \right).\\ \Rightarrow H\left( x \right) = A\left( x \right):\left( {3{x^2} + 2x - 5} \right)\\ \Rightarrow H\left( x \right) = \left( {3{x^4} + 11{x^3} - 5{x^2} - 19x + 10} \right):\left( {3{x^2} + 2x - 5} \right)\end{array}\)

Đặt phép tính chia để tìm H(x).

Lời giải chi tiết:

\(\begin{array}{l}A\left( x \right) = \left( {3{x^2} + 2x - 5} \right).H\left( x \right).\\ \Rightarrow H\left( x \right) = A\left( x \right):\left( {3{x^2} + 2x - 5} \right)\\ \Rightarrow H\left( x \right) = \left( {3{x^4} + 11{x^3} - 5{x^2} - 19x + 10} \right):\left( {3{x^2} + 2x - 5} \right)\end{array}\)

Vậy \(H\left( x \right) = {x^2} + 3x - 2\). 

-- Mod Toán 7 HỌC247