Giải bài 59 trang 56 SBT Toán 7 Cánh diều tập 2 - CD

Phương pháp giải

Thực hiện phép chia hai đa thức một biến theo quy tắc với \(Q(x) = R(x):P(x)\)

Lời giải chi tiết

Ta có: P(x) . Q(x) = R(x) \( \Rightarrow Q(x) = R(x):P(x)\)

a) \(Q(x) = R(x):P(x)\)\( = ( - {x^3} + 8):(x - 2)\)

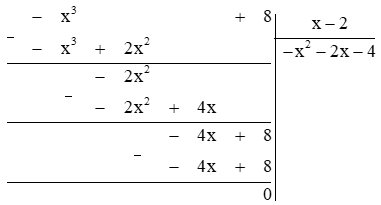
Vậy \(Q(x) =  - {x^2} - 2x - 4\)

b) \(Q(x) = R(x):P(x)\)\( = (10 - 13x + 2{x^2} + {x^3}):({x^2} - 3x + 2)\)\( = ({x^3} + 2{x^2} - 13x + 10):({x^2} - 3x + 2)\)

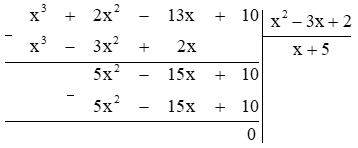
Vậy \(Q(x) = x + 5\)

-- Mod Toán 7 HỌC247