Giải bài 31 trang 77 SBT Toán 7 Cánh diều tập 2 - CD

Phương pháp giải

Xem các điều kiện đề bài đưa ra để tìm ra các phát biểu sai.

Lời giải chi tiết

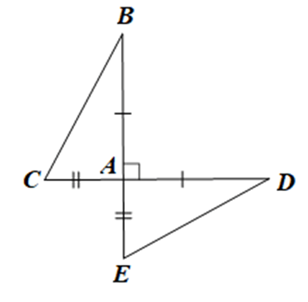
Xét ΔAED và ΔACB có:

\(\widehat {DA{\rm{E}}} = \widehat {BAC}\) (cùng bằng 90°),

AD = AB (giả thiết),

AE = AC (giả thiết)

Do đó ΔAED = ΔACB (hai cạnh góc vuông) nên phát biểu a đúng.

Từ ΔAED = ΔACB, suy ra:

 DE = BC (hai cạnh tương ứng), nên phát biểu b đúng.

\(\widehat {ABC} = \widehat {A{\rm{DE}}}\) (hai góc tương ứng) nên phát biểu d sai.

Xét ΔACE và ΔABD, ta thấy hai tam giác này không có các cạnh bằng nhau, các góc bằng nhau. Do đó hai tam giác này không bằng nhau, nên phát biểu c sai.

Vậy phát biểu c, d là phát biểu sai.

-- Mod Toán 7 HỌC247