Giải bài 3.7 trang 37 SBT Toán 7 Kết nối tri thức tập 1 - KNTT

Phương pháp giải:

a) Tia Om là tia phân giác của góc xOz

b)

-\(\widehat {yOz} + \widehat {zOx} = {180^0}\)

- Tia On là tia phân giác của góc yOn

c)

-\(\widehat {xOm} + \widehat {mOy} = {180^0}\)

- Tia On nằmg giữa hai tia Oy và Om

Lời giải chi tiết:

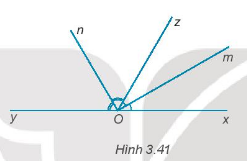
a)

Ta có: Tia Om là tia phân giác của góc xOz

\( \Rightarrow \widehat {xOm} = \widehat {mOz} = \dfrac{{\widehat {xOz}}}{2} = \dfrac{{{{60}^0}}}{2} = {30^0}\)

Vậy \(\widehat {xOm} = {30^0}\).

b)

Ta có: \(\widehat {yOz} + \widehat {zOx} = {180^0}\)(hai góc kề bù)

\(\begin{array}{l} \Rightarrow \widehat {yOz} + {60^0} = {180^0}\\ \Rightarrow \widehat {yOz} = {180^0} - {60^0}\\ \Rightarrow \widehat {yOz} = {120^0}\end{array}\)

Tia On là tia phân giác của góc yOn nên \(\widehat {yOn} = \widehat {nOz} = \dfrac{{\widehat {yOz}}}{2} = \dfrac{{{{120}^0}}}{2} = {60^0}\)

c)

Ta có: \(\widehat {xOm} + \widehat {mOy} = {180^0}\) (hai góc kề bù)

\( \Rightarrow {30^0} + \widehat {mOy} = {180^0} \Rightarrow \widehat {mOy} = {180^0} - {30^0} = {150^0}\)

Tia On nằm giữa hai tia Oy và Om nên:

\(\begin{array}{l}\widehat {yOn} + \widehat {nOm} = \widehat {yOm}\\ \Rightarrow {60^0} + \widehat {nOm} = {150^0}\\ \Rightarrow \widehat {nOm} = {150^0} - {60^0}\\ \Rightarrow \widehat {nOm} = {90^0}.\end{array}\) 

-- Mod Toán 7 HỌC247