Giải bài 28 trang 75 SBT Toán 7 Cánh diều tập 2
Cho góc xOy. Trên tia Ox lấy điểm C, trên tia Oy lấy điểm D sao cho OC = OD. Vẽ một phần đường tròn tâm C và tâm D có cùng bán kính, E là điểm chung của hai phần đường tròn đó (E nằm trong góc xOy) (Hình 15).
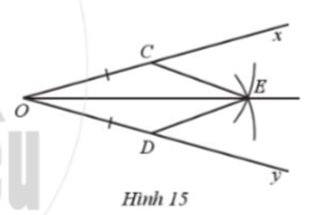
Vẽ các đoạn thẳng CE, DE. Chứng minh:
a) ΔOCE = ΔODE;
b) OE là tia phân giác của góc xOy;
c) \(\widehat {OCE} = \widehat {ODE}\)
Hướng dẫn giải chi tiết bài 28
Phương pháp giải
Xét các điều kiện về cạnh để chứng minh ΔOCE = ΔODE (c- c- c) từ đó suy ra các góc tương ứng bằng nhau nên OE là tia phân giác của góc xOy và \(\widehat {OCE} = \widehat {ODE}\)
Lời giải chi tiết
a) Vì E là điểm chung của hai phần đường tròn tâm C, tâm D có cùng bán kính nên EC = ED.
Xét ΔOCE và ΔODE có:
EC = ED (chứng minh trên),
OC = OD (giả thiết),
OE là cạnh chung.
Suy ra ΔOCE = ΔODE (c.c.c).
Vậy ΔOCE = ΔODE.
b) Vì ΔOCE = ΔODE(chứng minh câu a).
Nên \(\widehat {COE} = \widehat {DOE}\) (hai góc tương ứng).
Suy ra OE là tia phân giác của góc xOy.
Vậy OE là tia phân giác của góc xOy.
c) Vì ∆OCE = ∆ODE (chứng minh câu a)
Nên \(\widehat {OCE} = \widehat {ODE}\) (hai góc tương ứng).
Vậy \(\widehat {OCE} = \widehat {ODE}\)
-- Mod Toán 7 HỌC247
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.





