Giải bài 102 trang 98 SBT Toán 7 Cánh diều tập 2
Cho tam giác ABC và điểm G nằm trong tam giác. Chứng minh: Nếu diện tích các tam giác GAB, GBC và GCA bằng nhau thì G là trọng tâm của tam giác đó.
Hướng dẫn giải chi tiết Bài 102
Phương pháp giải
Áp dụng diện tích của ba tam giác GAB, GBC, GCA bằng nhau, hai tam giác bằng nhau để chứng minh AN là đường trung tuyến của tam giác ABC và CG cũng là trung tuyến của tam giác ABC
Lời giải chi tiết
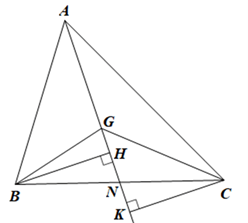
Gọi N là giao điểm của AG và BC.
Kẻ BH ⊥ AN (H ∈ AN) và CK ⊥ AN (K ∈ AN).
• Ta có:
\({S_{\Delta GAB}} = \frac{{AG.BH}}{2},{S_{\Delta GCA}} = \frac{{AG.CK}}{2}\)
Mà \({S_{\Delta AGB}} = {S_{\Delta AGC}}\) nên \(\frac{{AG.BH}}{2} = \frac{{AG.CK}}{2}\)
Suy ra BH = CK.
•Xét DBHN và DCKN có
\(\widehat {BHN} = \widehat {CKN}\left( { = 90^\circ } \right)\)
BH = CK (chứng minh trên),
\(\widehat {HNB} = \widehat {KNC}\) (hai góc đối đỉnh)
Do đó ∆BHN = ∆CKN (g.c.g)
Suy ra BN = CN (hai cạnh tương ứng)
Hay AN là đường trung tuyến của tam giác ABC.
•Chứng minh tương tự, ta có CG cũng là đường trung tuyến của tam giác ABC.
Tam giác ABC có AN, CG là hai đường trung tuyến cuả tam giác
Mà AN và CG cắt nhau tại G nên G là trọng tâm của tam giác ABC.
Vậy nếu diện tích các tam giác GAB, GBC và GCA bằng nhau thì G là trọng tâm của tam giác đó.
-- Mod Toán 7 HỌC247
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.





