Hướng dẫn Giải bài tập Toán 7 Cánh diều Chương 7 Bài 12 Tính chất ba đường trung trực của tam giác giúp các em học sinh nắm vững phương pháp giải bài tập và ôn luyện tốt kiến thức.
-
Câu hỏi khởi động trang 112 SGK Toán 7 Cánh diều tập 2 - CD
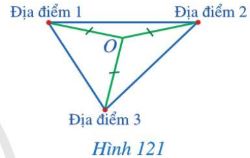
Hình 121 minh họa biển giới thiệu quần thể di tích, danh thắng cấp Quốc gia núi Dũng Quyết và khu vực Phượng Hoàng Trung Đô ở tỉnh Nghệ An (Hình 120).
Làm thế nào để xác định được vị trí cách đều ba địa điểm được minh họa trong Hình 121?
-
Hoạt động 1 trang 112 SGK Toán 7 Cánh diều tập 2 - CD
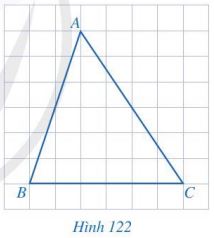
Cho tam giác ABC như Hình 122. Vẽ đường trung trực d của đoạn thẳng BC.
-
Luyện tập 1 trang 113 SGK Toán 7 Cánh diều tập 2 - CD
Cho tam giác ABC cân tại A. Vẽ đường phân giác AD. Chứng minh AD cũng là đường trung trực của tam giác ABC.
-
Hoạt động 2 trang 113 SGK Toán 7 Cánh diều tập 2 - CD
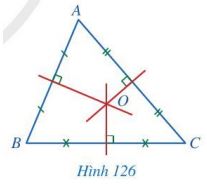
Quan sát các đường trung trực của tam giác ABC (Hình 126), cho biết ba đường trung trực đó có cùng đi qua một điểm hay không
-
Luyện tập 2 trang 114 SGK Toán 7 Cánh diều tập 2 - CD
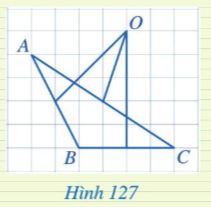
Trong Hình 127, điểm O có phải là giao điểm của ba đường trung trực của tam giác ABC không?
-
Giải bài 1 trang 115 SGK Toán 7 Cánh diều tập 2 - CD
Cho tam giác ABC và điểm O thỏa mãn OA = OB = OC. Chứng minh rằng O là giao điểm của ba đường trung trực của tam giác ABC.
-
Giải bài 2 trang 115 SGK Toán 7 Cánh diều tập 2 - CD
Cho tam giác ABC. Vẽ điểm O cách đều ba đỉnh A, B, C trong mỗi trường hợp sau:
a) Tam giác ABC nhọn;
b) Tam giác ABC vuông tại A;
c) Tam giác ABC có góc A tù.
-
Giải bài 3 trang 115 SGK Toán 7 Cánh diều tập 2 - CD
Tam giác ABC có ba đường trung tuyến cắt nhau tại G. Biết rằng điểm G cũng là giao điểm của ba đường trung trực trong tam giác ABC. Chứng minh tam giác ABC đều.
-
Giải bài 4 trang 115 SGK Toán 7 Cánh diều tập 2 - CD
Tam giác ABC có ba đường phân giác cắt nhau tại I. Biết rằng I cũng là giao điểm ba đường trung trực của tam giác ABC. Chứng minh tam giác ABC đều.
-
Giải bài 5 trang 115 SGK Toán 7 Cánh diều tập 2 - CD
Cho tam giác ABC. Đường trung trực của hai cạnh AB và AC cắt nhau tại điểm O nằm trong tam giác. M là trung điểm của BC. Chứng minh:
a) \(OM \bot BC\);
b) \(\widehat {MOB} = \widehat {MOC}\).
-
Giải bài 85 trang 94 SBT Toán 7 Cánh diều tập 2 - CD
Cho hai tam giác đều chung đáy ABC và BCD. Gọi I là trung điểm của BC. Trong các phát biểu sau, phát biểu nào đúng, phát biểu nào sai?
a) Đường thẳng BC là đường trung trực của AD.
b) Điểm I cách đều các điểm A, B, D.
c) Điểm B nằm trên đường trung trực của CD.
d) Điểm C không nằm trên đường trung trực của BD.
-
Giải bài 86 trang 94 SBT Toán 7 Cánh diều tập 2 - CD
Cho tam giác ABC cân ở A. Đường trung trực của cạnh AC cắt AB tại D. Biết CD là tia phân giác của góc ACB. Tính số đo các góc của tam giác ABC.
-
Giải bài 87 trang 94 SBT Toán 7 Cánh diều tập 2 - CD
Cho tam giác đều ABC có I là điểm cách đều ba cạnh AB, BC, CA. Chứng minh rằng I cách đều ba đỉnh A, B, C và cũng là trọng tâm của tam giác ABC.
-
Giải bài 88 trang 94 SBT Toán 7 Cánh diều tập 2 - CD
Chứng minh rằng các đường trung trực của tam giác vuông đi qua trung điểm của cạnh huyền.
-
Giải bài 89 trang 94 SBT Toán 7 Cánh diều tập 2 - CD
Cho góc nhọn xOy và điểm M nằm trong góc xOy. Gọi E, F là hai điểm nằm ngoài góc xOy sao cho Ox là đường trung trực của đoạn thẳng ME, Oy là đường trung trực của đoạn thẳng MF (Hình 55).
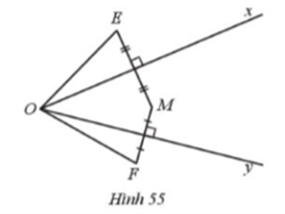
Chứng minh:
a) O là giao điểm ba đường trung trực của tam giácEMF.
b) Nếu \(\widehat {xOy} = 30^\circ \) thì \(\widehat {EOF} = 60^\circ \).
-
Giải bài 90 trang 95 SBT Toán 7 Cánh diều tập 2 - CD
Cho tam giác ABC cân ở A có \(\widehat {BAC} = 120^\circ \). Đường trung trực của các cạnh AB và AC cắt nhau ở I và cắt cạnh BC lần lượt tại D, E (Hình 56).
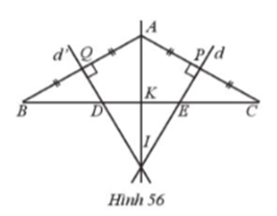
a) Chứng minh điểm I nằm trên đường trung trực của đoạn thẳng DE.
b) Đường tròn tâm I bán kính IA đi qua những điểm nào?
c) Tính số đo các góc của tam giác IBC.
-
Giải bài 91 trang 95 SBT Toán 7 Cánh diều tập 2 - CD
Cho tam giác ABC vuông cân ở A có đường phân giác AM. Gọi E là điểm nằm giữa B và C. Vẽ BH và CK vuông góc với AE (H, K thuộc AE).
a) Chứng minh ba đường trung trực tương ứng của các đoạn thẳng AB, AC, KH cùng đi qua điểm M.
b) Tính số đo các góc của tam giác MKH.