Luyện tập 1 trang 40 SGK Toán 11 Kết nối tri thức tập 2
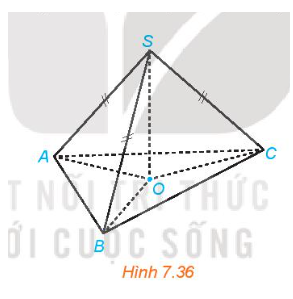
Cho hình chóp S.ABC có SA = SB = SC. Gọi O là hình chiếu của S trên mặt phẳng (ABC) (H.7.36).
a) Chứng minh rằng O là tâm đường tròn ngoại tiếp tam giác ABC.
b) Xác định hình chiếu của đường thẳng SA trên mặt phẳng (ABC).
c) Chứng minh rằng nếu AO⊥BC thìSA⊥BC.
d) Xác định hình chiếu của các tam giác SBC, SCA, SAB trên mặt phẳng (ABC)
Hướng dẫn giải chi tiết Luyện tập 1
Phương pháp giải
HS xem lại lý thuyết các bài đã học để trả lời câu hỏi này nhé.
Lời giải chi tiết
a) Ta có SA = SB = SC (điều kiện của đề bài).
Khi đó, OA, OB, OC đều là hình chiếu của S lên đường thẳng (ABC) theo các đỉnh tương ứng A, B, C.
Vì SA = SB = SC, ta có thể suy ra rằng OA, OB, OC đều nằm trên đường trung trực của đoạn thẳng BC, CA, AB tương ứng.
Khi đó, ta có OA = OB = OC, và O nằm trên đường trung trực của đoạn thẳng BC, CA, AB, nên O là tâm đường tròn ngoại tiếp tam giác ABC.
Vậy, ta đã chứng minh được rằng O là tâm đường tròn ngoại tiếp tam giác ABC.
b) Hình chiếu của đường thẳng SA trên mặt phẳng (ABC) là đoạn thẳng AB, vì SA vuông góc với mặt phẳng (ABC) và AB là một cạnh của tam giác đều ABC.
c) Nếu b⊥a thì b sẽ cắt M'N' tại một điểm D nằm trên AC, và do đó b//M′N′.
d) Gọi M,N,P lần lượt là hình chiếu vuông góc của S lên BC,CA,AB.
Do SA vuông góc với OM và SA song song với đường thẳng d nên d cũng vuông góc với OM.
Khi đó, hình chiếu của tam giác SBC lên mặt phẳng (ABC) là tam giác có đỉnh M và đường cao là đường thẳng d.
Tương tự, ta có thể tìm hình chiếu của tam giác SCA lên (ABC) là tam giác có đỉnh N và đường cao là đường thẳng e đi qua N và song song với SB, cũng như tìm hình chiếu của tam giác SAB lên (ABC) là tam giác có đỉnh P và đường cao là đường thẳng f đi qua P và song song với SC.
-- Mod Toán 11 HỌC247
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.
Bài tập SGK khác
Hoạt động 1 trang 38 SGK Toán 11 Kết nối tri thức tập 2 - KNTT
Hoạt động 2 trang 39 SGK Toán 11 Kết nối tri thức tập 2 - KNTT
Hoạt động 3 trang 40 SGK Toán 11 Kết nối tri thức tập 2 - KNTT
Vận dụng trang 41 SGK Toán 11 Kết nối tri thức tập 2 - KNTT
Khám phá trang 42 SGK Toán 11 Kết nối tri thức tập 2 - KNTT
Trải nghiệm trang 42 SGK Toán 11 Kết nối tri thức tập 2 - KNTT
Giải Bài 7.10 trang 42 SGK Toán 11 Kết nối tri thức tập 2 - KNTT
Giải Bài 7.11 trang 42 SGK Toán 11 Kết nối tri thức tập 2 - KNTT
Giải Bài 7.12 trang 42 SGK Toán 11 Kết nối tri thức tập 2 - KNTT
Giải Bài 7.13 trang 43 SGK Toán 11 Kết nối tri thức tập 2 - KNTT
Giải Bài 7.14 trang 43 SGK Toán 11 Kết nối tri thức tập 2 - KNTT
Giải Bài 7.15 trang 43 SGK Toán 11 Kết nối tri thức tập 2 - KNTT
Bài tập 7.13 trang 30 SBT Toán 11 Tập 2 Kết nối tri thức - KNTT
Bài tập 7.14 trang 30 SBT Toán 11 Tập 2 Kết nối tri thức - KNTT
Bài tập 7.15 trang 30 SBT Toán 11 Tập 2 Kết nối tri thức - KNTT
Bài tập 7.16 trang 31 SBT Toán 11 Tập 2 Kết nối tri thức - KNTT
Bài tập 7.17 trang 31 SBT Toán 11 Tập 2 Kết nối tri thức - KNTT
Bài tập 7.18 trang 31 SBT Toán 11 Tập 2 Kết nối tri thức -