Bài tập 7.13 trang 30 SBT Toán 11 Tập 2 Kết nối tri thức
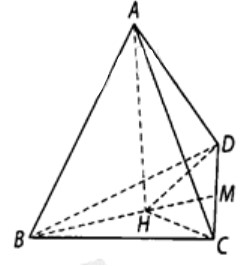
Cho tứ diện \(ABCD\) có tất cả các cạnh bằng nhau và bằng \(a\). Tính côsin của góc giữa đường thẳng \(AB\) và mặt phẳng \(BCD\)?
Hướng dẫn giải chi tiết Bài 7.13
Kẻ \(AH \bot \left( {BCD} \right)\) tại \(H\).
Ta có: \(BH\) là hình chiếu vuông góc của \(AB\) trên mặt phẳng \(\left( {BCD} \right)\).
Nên góc giữa đường thẳng \(AB\) và mặt phẳng \(\left( {BCD} \right)\) bằng góc giữa hai đường thẳng \(AB\) và \(BH\).
Mà \(\left( {AB,BH} \right) = \widehat {ABH}\).
Vì \(AB = AC = AD\) nên \(HB = HC = HD\), hay \(H\) là tâm của tam giác\(BCD\).
Suy ra\(BH = \frac{2}{3}.\frac{{a\sqrt 3 }}{2} = \frac{{a\sqrt 3 }}{3}\).
Từ đó ta tính được: \(\cos \widehat {ABH} = \frac{{BH}}{{AB}} = \frac{{\sqrt 3 }}{3}\).
Vậy côsin của góc giữa đường thẳng \(AB\) và mặt phẳng \(\left( {BCD} \right)\) bằng \(\frac{{\sqrt 3 }}{3}\).
-- Mod Toán 11 HỌC247
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.
Bài tập SGK khác
Giải Bài 7.14 trang 43 SGK Toán 11 Kết nối tri thức tập 2 - KNTT
Giải Bài 7.15 trang 43 SGK Toán 11 Kết nối tri thức tập 2 - KNTT
Bài tập 7.14 trang 30 SBT Toán 11 Tập 2 Kết nối tri thức - KNTT
Bài tập 7.15 trang 30 SBT Toán 11 Tập 2 Kết nối tri thức - KNTT
Bài tập 7.16 trang 31 SBT Toán 11 Tập 2 Kết nối tri thức - KNTT
Bài tập 7.17 trang 31 SBT Toán 11 Tập 2 Kết nối tri thức - KNTT
Bài tập 7.18 trang 31 SBT Toán 11 Tập 2 Kết nối tri thức -





