Bài tập 7.17 trang 31 SBT Toán 11 Tập 2 Kết nối tri thức - KNTT

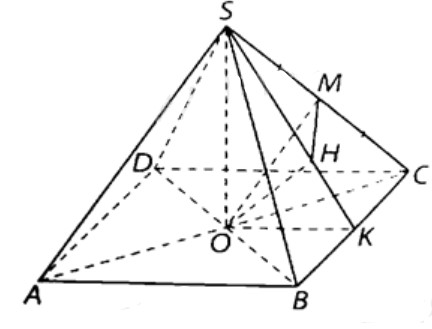
a) Ta có: \(SO \bot AC\); \(SO \bot BD\) nên \(SO \bot \left( {ABCD} \right)\).

b) Vì \(AO \bot \left( {SBD} \right)\) nên \(SO\) là hình chiếu vuông góc của \(SA\) trên mặt phẳng \(\left( {SBD} \right)\), do đó góc giữa đường thẳng \(SA\) và mặt phẳng \(\left( {SBD} \right)\) bằng góc giữa hai đường thẳng \(SA\) và \(SO\). Mà \(\left( {SA,SO} \right) = \widehat {ASO}\) nên góc giữa đường thẳng \(SA\) và mặt phẳng \(\left( {SBD} \right)\) bằng góc \(\widehat {ASO}\). Xét tam giác \(SAC\) có

\(S{A^2} + S{C^2} = A{C^2}\) và \(SA = SC\) nên tam giác \(SAC\) vuông cân tại \(S\), suy ra \(\widehat {ASO} = {45^ \circ }\). Vậy góc giữa đường thẳng \(SA\) và mặt phẳng \(\left( {SBD} \right)\) bằng \({45^ \circ }\).

c) Kẻ \(OK \bot BC\) tại \(K,OH \bot SK\) tại \(H\) thì ta chứng minh được \(OH \bot \left( {SBC} \right)\),

suy ra HM là hình chiếu vuông góc của \(OM\) trên mặt phẳng \(\left( {SBC} \right)\),

do đó góc giữa đường thẳng \(OM\) và mặt phẳng \(\left( {SBC} \right)\) bằng góc giữa hai đường thẳng \(OM\) và \(MH\),

mà \(\left( {OM,MH} \right) = \widehat {OMH}\) nên góc giữa đường thẳng \(OM\) và mặt phẳng (SBC) bằng góc \({\rm{OMH}}\) hay \(\widehat {{\rm{OMH}}}\). Ta có: \(OM = \frac{a}{2},OK = \frac{a}{2},SO = \frac{{a\sqrt 2 }}{2}\).

Tam giác SOK vuông tại \(O\), đường cao \({\rm{OH}}\) nên \({\rm{OH}} = \frac{{{\rm{SO}} \cdot {\rm{OK}}}}{{SK}} = \frac{{a\sqrt 6 }}{6}\).

Vì tam giác \(OMH\) vuông tại \(H\) nên \({\rm{sin}}\alpha = {\rm{sin}}\widehat {OMH} = \frac{{OH}}{{OM}} = \frac{{\sqrt 6 }}{3}\).

-- Mod Toán 11 HỌC247