Hoạt động 1 trang 28 SGK Toán 11 Kết nối tri thức tập 2
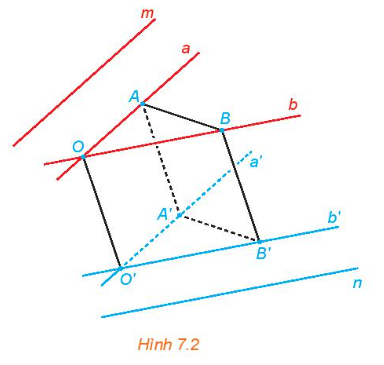
Trong không gian, cho hai đường thẳng chéo nhau m và n. Từ hai điểm phân biệt O,O' tuỳ ý lần lượt kẻ các cặp đường thẳng a, b và a',b' tương ứng song song với m, n (H.7.2).
a) Mỗi cặp đường thẳng a, a và b, b' có cùng thuộc một mặt phẳng hay không?
b) Lấy các điểm A, B (khác O) tương ứng thuộc a, b. Đường thẳng qua A song song với OO' cắt a' tại A, đường thẳng qua B song song với OO' cắt b' tại B' Giải thích vì sao OAA'O', OBB'O', ABB'A' là các hình bình hành.
c) So sánh góc giữa hai đường thẳng a, b và góc giữa hai đường thẳng a', b'. (Gợi ý: Áp dụng định lí côsin cho các tam giác OAB, O'A'B').
Hướng dẫn giải chi tiết Hoạt động 1
Phương pháp giải
HS xem lại lý thuyết Bài hai đường thẳng song song.
Lời giải chi tiết
a) Mỗi cặp đường thẳng a, a' và b, b' cùng thuộc một mặt phẳng. Vì a//a', b//b' khi đó (a,b)=(a,b')
b) Ta có :
\(\left\{\begin{matrix} OA // O'A' & & & \\ OB // O'B' & & & \\ AB//A'B' & & & \end{matrix}\right.\)
do đó OAA'O'' ; OBB'O' và ABB'A' là hình bình hành.
c) Áp dụng định lí côsin cho các tam giác OAB và O'A'B', ta có:
\(cos(a,b)=\frac{OA}{OB} cos (a',b')=\frac{O'A'}{O'B'}\)
vì O'A' = OA và O'B' = OB do a', b' là các đường song song với a, b, ta có:
\(cos(a,b)= cos (a',b')\)
-- Mod Toán 11 HỌC247
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.
Bài tập SGK khác
Vận dụng trang 29 SGK Toán 11 Kết nối tri thức tập 2 - KNTT
Hoạt động 2 trang 29 SGK Toán 11 Kết nối tri thức tập 2 - KNTT
Luyện tập 1 trang 30 SGK Toán 11 Kết nối tri thức tập 2 - KNTT
Giải Bài 7.1 trang 30 SGK Toán 11 Kết nối tri thức tập 2 - KNTT
Giải Bài 7.2 trang 30 SGK Toán 11 Kết nối tri thức tập 2 - KNTT
Giải Bài 7.3 trang 30 SGK Toán 11 Kết nối tri thức tập 2 - KNTT
Giải Bài 7.4 trang 30 SGK Toán 11 Kết nối tri thức tập 2 - KNTT
Bài tập 7.1 trang 25 SBT Toán 11 Tập 2 Kết nối tri thức - KNTT
Bài tập 7.2 trang 26 SBT Toán 11 Tập 2 Kết nối tri thức - KNTT
Bài tập 7.3 trang 26 SBT Toán 11 Tập 2 Kết nối tri thức - KNTT
Bài tập 7.4 trang 26 SBT Toán 11 Tập 2 Kết nối tri thức - KNTT
Bài tập 7.5 trang 26 SBT Toán 11 Tập 2 Kết nối tri thức - KNTT





