Bài tập 7.3 trang 26 SBT Toán 11 Tập 2 Kết nối tri thức
Cho tứ diện \(ABCD\), gọi \(M\) và \(N\) lần lượt là trung điểm của \(AC\) và \(BD\). Biết \(MN = a\sqrt 3 ;AB = 2\sqrt 2 a\) và \(CD = 2a\). Chứng minh rằng đường thẳng \(AB\) vuông góc với đường thẳng \(CD\)?
Hướng dẫn giải chi tiết Bài 7.3
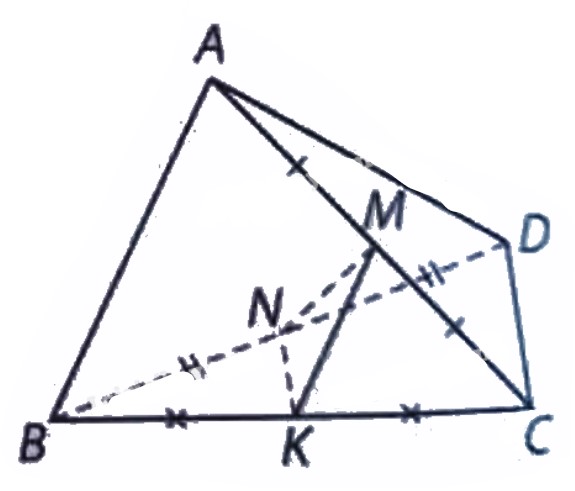
Lấy \(K\) là trung điểm của cạnh \(BC\).
Ta có: \(NK\) và \(MK\) lần lượt là đường trung bình của tam giác \(BCD\) và tam giác \(ABC\) nên \(NK = a,MK = a\sqrt 2 \).
Do đó, \(M{N^2} = 3{a^2} = N{K^2} + M{K^2}\).
Suy ra tam giác \(MNK\) vuông tại \(K\), hay \(MK \bot NK\), mà \(MK//AB\) và \(NK//CD\) nên:
\(\left( {AB,CD} \right) = \left( {MK,NK} \right) = {90^ \circ }\), hay \(AB \bot CD\).
-- Mod Toán 11 HỌC247
Nếu bạn thấy
hướng dẫn giải
Bài tập 7.3 trang 26 SBT Toán 11 Tập 2 Kết nối tri thức - KNTT HAY thì click chia sẻ
YOMEDIA
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.
