Giải Bài 9.5 trang 86 SGK Toán 11 Kết nối tri thức tập 2
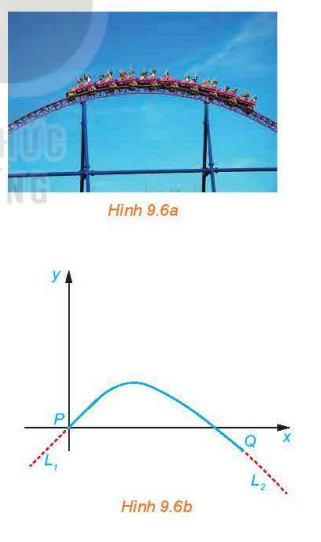
Một kĩ sư thiết kế một đường ray tàu lượn, mà mặt cắt của nó gồm một cung đường cong có dạng parabol (H.9.6a), đoạn dốc lên \(L_{1}\), và đoạn dốc xuống \(L_{2}\), là những phần đường thẳng có hệ số góc lần lượt là 0,5 và –0,75. Để tàu lượn chạy êm và không bị đổi hướng đột ngột, \(L_{1}\) và \(L_{2}\) phải là những tiếp tuyến của cung parabol tại các điểm chuyển tiếp P và Q (H.9.6b). Giả sử gốc toạ độ đặt tại P và phương trình của parabol là \(y = ax^{2} + bx + c\), trong đó x tính bằng mét.
a) Tìm c.
b) Tính y'(0) và tìm b.
c) Giả sử khoảng cách theo phương ngang giữa P và Q là 40 m. Tìm a.
d) Tìm chênh lệch độ cao giữa hai điểm chuyển tiếp P và Q.
Hướng dẫn giải chi tiết Bài 9.5
Phương pháp giải
Sử dụng phương trình tiếp tuyến của đồ thị hàm số tại điểm P(xo,yo) là
y - yo = f' (xo)( x − xo ),
trong đó yo = f(xo).
Lời giải chi tiết
a) Ta có
\(y' = 2ax + b\)
Ta lại có phương trình của tiếp tuyến là:
\(y-y_{p}=y'(x_{p})(x-x_{p})\)
Thay các giá trị này vào phương trình tiếp tuyến, ta có:
\(0=2ap+b\)
Vậy \(b=-2ap\) thay x=0 vào phương trình đường cong ta có
\(y=a(0)^{2}+c(0)+c=c \Rightarrow c=yp\)
b) \(y'=2ax+b=c\) khi \(x=0\Rightarrow y'(0)b\)
c) Ta có
\(y'(P)=2aP+b=0,5\)
\(y'(P)=2aP+b=0,75\)
Trừ hai phương trình, ta có:
\(2a(Q-P)=-1,25\)
\(Q-P=20\)
\(\Rightarrow a=\frac{-1,25}{40}\)
-- Mod Toán 11 HỌC247
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.
Bài tập SGK khác
Giải Bài 9.3 trang 86 SGK Toán 11 Kết nối tri thức tập 2 - KNTT
Giải Bài 9.4 trang 86 SGK Toán 11 Kết nối tri thức tập 2 - KNTT
Bài tập 9.1 trang 57 SBT Toán 11 Tập 2 Kết nối tri thức - KNTT
Bài tập 9.2 trang 57 SBT Toán 11 Tập 2 Kết nối tri thức - KNTT
Bài tập 9.3 trang 57 SBT Toán 11 Tập 2 Kết nối tri thức - KNTT
Bài tập 9.4 trang 57 SBT Toán 11 Tập 2 Kết nối tri thức - KNTT
Bài tập 9.5 trang 57 SBT Toán 11 Tập 2 Kết nối tri thức - KNTT
Bài tập 9.6 trang 57 SBT Toán 11 Tập 2 Kết nối tri thức - KNTT
Bài tập 9.7 trang 57 SBT Toán 11 Tập 2 Kết nối tri thức - KNTT
