Bài tập 44 trang 45 SBT Toán 11 Tập 2 Cánh diều

Lý thuyết10 Trắc nghiệm

37 BT SGK

0 FAQ

Lập bảng biến thiên và vẽ đồ thị hàm số:

a) \(y = {\left( {\sqrt 2 } \right)^x};\)

b) \(y = {\left( {\frac{1}{{\sqrt 2 }}} \right)^x};\)

c) \(y = {\log _{\sqrt 3 }}x;\)

d) \(y = - {\log _2}x.\)

Toán 11 Cánh Diều Chương 6 Bài 3 Trắc nghiệm Toán 11 Cánh Diều Chương 6 Bài 3 Giải bài tập Toán 11 Cánh Diều Chương 6 Bài 3

Hướng dẫn giải chi tiết Bài tập 44

a) Vì hàm số \(y = {\left( {\sqrt 2 } \right)^x}\) có cơ số \(\sqrt 2 > 1\) nên ta có bảng biến thiên như sau:

Đồ thị của hàm số \(y = {\left( {\sqrt 2 } \right)^x}\) là một đường cong liền nét đi qua các điểm \(\left( { - 2;\frac{1}{2}} \right),\left( {0;1} \right),\left( {2;2} \right),\left( {4;4} \right).\)

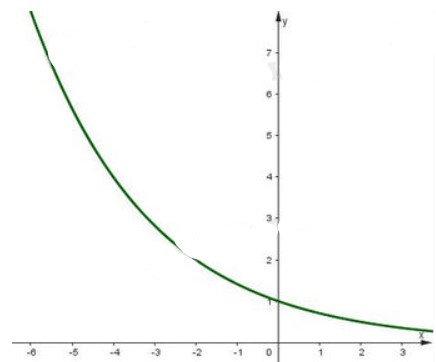
b) Vì hàm số \(y = {\left( {\frac{1}{{\sqrt 2 }}} \right)^x}\) có cơ số \(\frac{1}{{\sqrt 2 }} < 1\) nên ta có bảng biến thiên như sau:

Đồ thị của hàm số \(y = {\left( {\frac{1}{{\sqrt 2 }}} \right)^x}\) là một đường cong liền nét đi qua các điểm \(\left( { - 4;4} \right),\left( { - 2;2} \right),\left( {0;1} \right),\left( {2;\frac{1}{2}} \right).\)

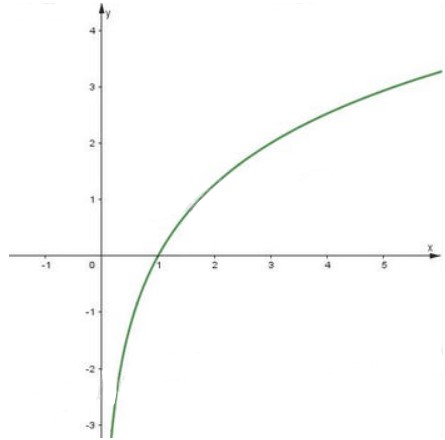
c) Vì hàm số \(y = {\log _{\sqrt 3 }}x\) có cơ số \[\sqrt 3 > 1\] nên ta có bảng biến thiên như sau:

Đồ thị của hàm số \(y = {\log _{\sqrt 3 }}x\) là một đường cong liền nét đi qua các điểm \(\left( {\frac{1}{3}; - 2} \right),\left( {1;0} \right),\left( {3;2} \right),\left( {9;4} \right).\)

d) Vì hàm số \(y = - {\log _2}x\) có cơ số \(2 > 1\) nên ta có bảng biến thiên như sau:

Đồ thị của hàm số \(y = - {\log _2}x\) là một đường cong liền nét đi qua các điểm \(\left( {\frac{1}{2};1} \right),\left( {1;0} \right),\left( {2; - 1} \right),\left( {4; - 2} \right).\)