Giải bài 1.30 tr 37 SBT Hình học 11
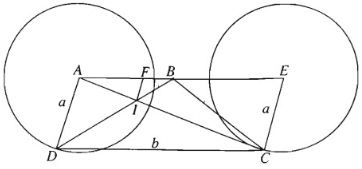
Cho hình thang ABCD có AB song song với CD, AD = a, DC = b còn hai đỉnh A, B cố định. Gọi I là giao điểm của hai đường chéo.
a) Tìm tập hợp các điểm C khi D thay đổi.
b) Tìm tập hợp các điểm I khi C và D thay đổi như trong câu a).
Hướng dẫn giải chi tiết
a) Dựng hình bình hành ADCE. Ta có \(\overrightarrow {DC} = \overrightarrow {AE} \) không đổi.
Do AE = b không đổi, nên E cố định. Do AD = EC = a nên khi D chạy trên đường tròn (A;a) thì C chạy trên đường tròn (E;a) là ảnh của (A;a) qua phép tịnh tiến theo \(\overrightarrow {AE} \).
b) Đường thẳng qua I , song song với AD cắt AE tại F.
Ta có :
\(\begin{array}{l}
\frac{{AI}}{{IC}} = \frac{{AB}}{{CD}}\\
\Rightarrow \frac{{AI}}{{AI + IC}} = \frac{{AB}}{{AB + b}}\\
\Rightarrow \frac{{AI}}{{AC}} = \frac{{AB}}{{AB + b}}\\
\Rightarrow \overrightarrow {AI} = \frac{{AB}}{{AB + b}}\overrightarrow {AC}
\end{array}\)
Do đó có thể xem I là ảnh của C qua phép vị tự tâm A, tỉ số \(\frac{{AB}}{{AB + b}}\). Vậy khi C chạy trên (E;a) thì I chạy trên đường tròn là ảnh của (E;a) qua phép vị tự nói trên.
-- Mod Toán 11 HỌC247
-


Cho hình chữ nhật ABCD tâm I. Gọi E, F, G, H lần lượt là trung điểm của AB, CD, CI, FC. Phép đồng dạng hợp thành bởi phép vị tự tâm C tỉ số k = 2 và phép đối xứng tâm I biến tứ giác IGHF thành:
bởi Long lanh
 22/01/2021
22/01/2021
A. AIFD
B. BCFI
C. CIEB
D. DIEA
Theo dõi (0) 1 Trả lời -


Tính độ dài đoạn thẳng M'N' biết phép đồng dạng F tỉ số k=căn 5 biến 2 điểm M (-1,1) và N(0,3) lần lượt thành M' và N'
bởi Trần Thanh Thảo
 29/12/2019
Trong mặt phẳng tọa độ Oxy, phép đồng dạng F tỉ số k = căn 5 biến 2 điểm M(-1,1) và N(0,3) lần lượt thành M' N'. Tính độ dài M' N'Theo dõi (0) 0 Trả lời
29/12/2019
Trong mặt phẳng tọa độ Oxy, phép đồng dạng F tỉ số k = căn 5 biến 2 điểm M(-1,1) và N(0,3) lần lượt thành M' N'. Tính độ dài M' N'Theo dõi (0) 0 Trả lời