Bài 5 trang 100 SGK Toán 11 Cánh diều Tập 1 - CD

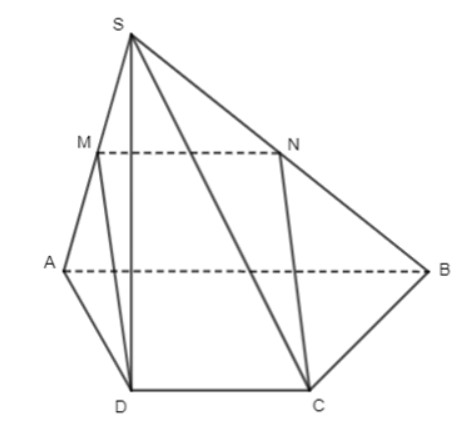
Trong mặt phẳng \((SAB)\), có: M, N lần lượt là trung điểm của SA và SB

Do đó MN là đường trung bình của tam giác

Suy ra \(MN // AB\) và MN = $\frac{1}{2}$ AB.

Lại có \(AB // CD\) (do \(ABCD\) là hình thang) và \(AB = 2CD\) hay CD = $\frac{1}{2}$ AB

Do đó \(MN // CD\) và \(MN = CD\).

Suy ra \(MNCD\) là hình bình hành.

Vì vậy \(MD // NC\).

-- Mod Toán 11 HỌC247