Bài 7 trang 100 SGK Toán 11 Cánh diều Tập 1 - CD

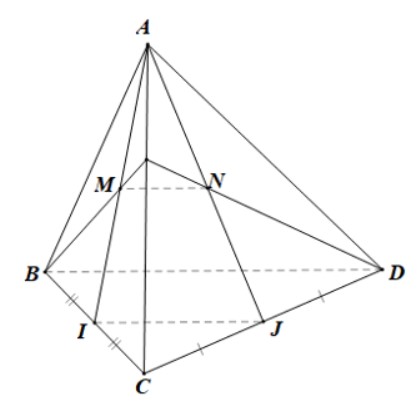
- Ta có: \(B ∈ (BDK)\) và \(B ∈ (BCD)\) nên B là giao điểm của \((BDK)\) và \((BCD)\).

            \(D ∈ (BDK)\) và \(D ∈ (BCD)\) nên D là giao điểm của \((BDK)\) và \((BCD)\).

Do đó \((BDK) ∩ (BCD) = BD\).

- Ta có: \(M ∈ BK\) mà \(BK ⊂ (BDK)\) nên \(M ∈ (BDK)\); 

            \(M ∈ AI\) mà \(AI ⊂ (AIJ)\) nên \(M ∈ (AIIJ)\)

Do đó M là giao điểm của \((BDK)\) và \((AIJ)\)

Tương tự ta cũng có N là giao điểm của \((BDK)\) và \((AIJ)\)

Suy ra \((BDK) ∩ (AIJ) = MN\).

- Ta có: \(I ∈ BC\) mà \(BC ⊂ (BCD)\) nên \(I ∈ (BCD)\)

Lại có \(I ∈ (AIJ)\) nên I là giao điểm của \((BCD)\) và \((AIJ)\)

Tương tự ta cũng có J là giao điểm của \((BCD)\) và \((AIJ)\)

Suy ra \((BCD) ∩ (AIJ) = IJ\).

- Xét \(DBCD\) có I, J lần lượt là trung điểm của BC, CD nên IJ là đường trung bình của tam giác

Do đó \(IJ // BD\).

- Ta có: \((BDK) ∩ (BCD) = BD\);

            \((BDK) ∩ (AIJ) = MN\);

            \((BCD) ∩ (AIJ) = IJ\);

            \( IJ // BD\).

Suy ra \(MN // BD\).

-- Mod Toán 11 HỌC247