B├Āi giß║Żng Biß║┐n cß╗æ giao v├Ā quy tß║»c nh├ón x├Īc suß║źt chŲ░ŲĪng tr├¼nh To├Īn 11 s├Īch SGK Ch├ón trß╗Øi s├Īng tß║Īo sß║Į gi├║p c├Īc em nß║»m ─æŲ░ß╗Żc c├Īc kh├Īi niß╗ćm mß╗øi vß╗ü biß║┐n cß╗æ v├Ā quy tß║»c nh├ón x├Īc suß║źt cß╗¦a hai biß║┐n cß╗æ ─æß╗Öc lß║Łp.
T├│m tß║»t l├Į thuyß║┐t
1.1. Biến cố giao
Cho hai biß║┐n cß╗æ A v├Ā B. Biß║┐n cß╗æ "Cß║Ż A v├Ā B c├╣ng xß║Ży ra", k├Ł hiß╗ću AB hoß║Ęc A\(\cap\)B ─æŲ░ß╗Żc gß╗Źi l├Ā biß║┐n cß╗æ giao cß╗¦a A v├Ā B.
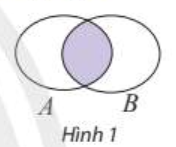
Ch├║ ├Į: Tß║Łp hß╗Żp m├┤ tß║Ż biß║┐n cß╗æ AB l├Ā giao cß╗¦a hai tß║Łp hß╗Żp m├┤ tß║Ż biß║┐n cß╗æ A v├Ā biß║┐n cß╗æ B. Biß║┐n cß╗æ AB xß║Ży ra khi v├Ā chß╗ē khi cß║Ż hai biß║┐n cß╗æ A v├Ā B xß║Ży ra.
1.2. Hai biến cố xung khắc
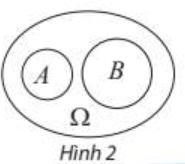
Hai biß║┐n cß╗æ A v├Ā B ─æŲ░ß╗Żc gß╗Źi l├Ā xung khß║»c nß║┐u A v├Ā B kh├┤ng ─æß╗ōng thß╗Øi xß║Ży ra.
Ch├║ ├Į: Hai biß║┐n cß╗æ A v├Ā B l├Ā xung khß║»c khi v├Ā chß╗ē khi A \(\cap\) B =\(\emptyset\).
1.3. Biß║┐n cß╗æ ─æß╗Öc lß║Łp
Hai biß║┐n cß╗æ A v├Ā B ─æŲ░ß╗Żc gß╗Źi l├Ā ─æß╗Öc lß║Łp nß║┐u viß╗ćc xß║Ży ra hay kh├┤ng xß║Ży ra cß╗¦a biß║┐n cß╗æ n├Āy kh├┤ng l├Ām ß║Żnh hŲ░ß╗¤ng tß╗øi x├Īc suß║źt xß║Ży ra cß╗¦a biß║┐n cß╗æ kia.
Nhß║Łn x├®t: Nß║┐u hai biß║┐n cß╗æ A v├Ā B ─æß╗Öc lß║Łp th├¼ A v├Ā \(\bar B\); \(\bar A\) v├Ā B; \(\bar A\) v├Ā \(\bar B\) c┼®ng ─æß╗Öc lß║Łp.
1.4. Quy tß║»c nh├ón x├Īc suß║źt cß╗¦a hai biß║┐n cß╗æ
Nß║┐u hai biß║┐n cß╗æ A v├Ā B ─æß╗Öc lß║Łp vß╗øi nhau th├¼
P(AB) = P(A).P(B).
C├┤ng thß╗®c n├Āy gß╗Źi l├Ā c├┤ng thß╗®c nh├ón x├Īc suß║źt cho hai biß║┐n cß╗æ ─æß╗Öc lß║Łp.
Ch├║ ├Į: Vß╗øi hai biß║┐n cß╗æ A v├Ā B, nß║┐u P(AB) \(\ne\) P(A)P(B) th├¼ A v├Ā B kh├┤ng ─æß╗Öc lß║Łp.
B├Āi tß║Łp minh hß╗Źa
C├óu 1: Mß╗Öt chiß║┐c ├┤t├┤ vß╗øi hai ─æß╗Öng cŲĪ ─æß╗Öc lß║Łp ─æang gß║Ęp trß╗źc trß║Ęc k─® thuß║Łt. X├Īc suß║źt ─æß╗ā ─æß╗Öng cŲĪ 1 gß║Ęp trß╗źc trß║Ęc l├Ā 0,5. X├Īc suß║źt ─æß╗ā ─æß╗Öng cŲĪ 2 gß║Ęp trß╗źc trß║Ęc l├Ā 0,4. Biß║┐t rß║▒ng xe chß╗ē kh├┤ng thß╗ā chß║Īy ─æŲ░ß╗Żc khi cß║Ż hai ─æß╗Öng cŲĪ bß╗ŗ hß╗Ång. T├Łnh x├Īc suß║źt ─æß╗ā xe ─æi ─æŲ░ß╗Żc.
HŲ░ß╗øng dß║½n giß║Żi:
Gß╗Źi A l├Ā biß║┐n cß╗æ ŌĆ£─æß╗Öng cŲĪ 1 bß╗ŗ hß╗ÅngŌĆØ, gß╗Źi B l├Ā biß║┐n cß╗æ ŌĆ£─æß╗Öng cŲĪ 2 bß╗ŗ hß╗ÅngŌĆØ.
Suy ra AB l├Ā biß║┐n cß╗æ ŌĆ£cß║Ż hai ─æß╗Öng cŲĪ bß╗ŗ hß╗ÅngŌĆØ Ōćö ŌĆ£ xe kh├┤ng chß║Īy ─æŲ░ß╗Żc nß╗»aŌĆØ.
Lß║Īi thß║źy hai ─æß╗Öng cŲĪ hoß║Īt ─æß╗Öng ─æß╗Öc lß║Łp n├¬n A v├Ā B l├Ā hai biß║┐n cß╗æ ─æß╗Öc lß║Łp.
├üp dß╗źng quy tß║»c nh├ón x├Īc suß║źt ta ─æŲ░ß╗Żc x├Īc suß║źt ─æß╗ā xe phß║Żi dß╗½ng lß║Īi giß╗»a ─æŲ░ß╗Øng l├Ā P(AB) = 0,5.0,4 = 0,2.
Vß║Ły x├Īc suß║źt ─æß╗ā xe ─æi ─æŲ░ß╗Żc l├Ā 1ŌłÆ0,2=0,8.
C├óu 2: X├Īc suß║źt bß║»n tr├║ng ─æ├Łch cß╗¦a mß╗Öt ngŲ░ß╗Øi bß║»n s├║ng l├Ā 0,6. X├Īc suß║źt ─æß╗ā trong ba lß║¦n bß║»n ─æß╗Öc lß║Łp ngŲ░ß╗Øi ─æ├│ bß║»n tr├║ng ─æ├Łch ─æ├║ng mß╗Öt lß║¦n.
HŲ░ß╗øng dß║½n giß║Żi:
Gß╗Źi A l├Ā biß║┐n cß╗æ ŌĆ£ngŲ░ß╗Øi bß║»n s├║ng bß║»n tr├║ng ─æ├ŁchŌĆØ. Ta c├│ P(A)=0,6.
Suy ra \(\bar A\) l├Ā biß║┐n cß╗æ ŌĆ£ngŲ░ß╗Øi bß║»n s├║ng kh├┤ng bß║»n tr├║ng ─æ├ŁchŌĆØ. Ta c├│ P(\(\bar A\))=0,4
X├®t ph├®p thß╗Ł ŌĆ£bß║»n ba lß║¦n ─æß╗Öc lß║ŁpŌĆØ vß╗øi biß║┐n cß╗æ ŌĆ£ngŲ░ß╗Øi ─æ├│ bß║»n tr├║ng ─æ├Łch ─æ├║ng mß╗Öt lß║¦nŌĆØ, ta c├│ c├Īc biß║┐n cß╗æ xung khß║»c sau:
B: ŌĆ£Bß║»n tr├║ng ─æ├Łch lß║¦n ─æß║¦u v├Ā trŲ░ß╗Żt ß╗¤ hai lß║¦n bß║»n sauŌĆØ. Ta c├│ P(B) = 0,6.0,4.0,4 = 0,096
C: ŌĆ£Bß║»n tr├║ng ─æ├Łch ß╗¤ lß║¦n bß║»n thß╗® hai v├Ā trŲ░ß╗Żt ß╗¤ lß║¦n ─æß║¦u v├Ā lß║¦n thß╗® baŌĆØ. Ta c├│
P(C) = 0,4.0,6.0,4 = 0,096
D: ŌĆ£Bß║»n tr├║ng ─æ├Łch ß╗¤ lß║¦n bß║»n thß╗® ba v├Ā trŲ░ß╗Żt ß╗¤ hai lß║¦n ─æß║¦uŌĆØ. Ta c├│:
P(D) = 0,4.0,4.0,6 = 0,096
X├Īc suß║źt ─æß╗ā ngŲ░ß╗Øi ─æ├│ bß║»n tr├║ng ─æ├Łch ─æ├║ng mß╗Öt lß║¦n l├Ā:
P = P(A)+P(B)+P(C) = 0,096+0,096+0,096=0,288
Luyß╗ćn tß║Łp B├Āi 1 To├Īn 11 Ch├ón Trß╗Øi S├Īng Tß║Īo
Hß╗Źc xong b├Āi hß╗Źc n├Āy, em c├│ thß╗ā:
- Nhß║Łn biß║┐t ─æŲ░ß╗Żc kh├Īi niß╗ćm vß╗ü x├Īc suß║źt cß╗Ģ ─æiß╗ān: giao c├Īc biß║┐n cß╗æ; biß║┐n cß╗æ ─æß╗Öc lß║Łp.
- T├Łnh ─æŲ░ß╗Żc x├Īc suß║źt cß╗¦a biß║┐n cß╗æ hß╗Żp bß║▒ng c├Īch sß╗Ł dß╗źng c├┤ng thß╗®c nh├ón (cho trŲ░ß╗Øng hß╗Żp biß║┐n cß╗æ ─æß╗Öc lß║Łp), phŲ░ŲĪng ph├Īp tß╗Ģ hß╗Żp, sŲĪ ─æß╗ō h├¼nh c├óy.
3.1. Trß║»c nghiß╗ćm B├Āi 1 To├Īn 11 Ch├ón Trß╗Øi S├Īng Tß║Īo
C├Īc em c├│ thß╗ā hß╗ć thß╗æng lß║Īi nß╗Öi dung kiß║┐n thß╗®c ─æ├Ż hß╗Źc ─æŲ░ß╗Żc th├┤ng qua b├Āi kiß╗ām tra Trß║»c nghiß╗ćm To├Īn 11 Ch├ón trß╗Øi s├Īng tß║Īo ChŲ░ŲĪng 9 B├Āi 1 cß╗▒c hay c├│ ─æ├Īp ├Īn v├Ā lß╗Øi giß║Żi chi tiß║┐t.
-
- A. \(\frac{8}{169}\).
- B. \(\frac{1}{13}\).
- C. \(\frac{1}{169}\).
- D. \(\frac{2}{13}\).
-
- A. \({{A}_{1}}{{A}_{2}}{{A}_{3}}\).
- B. \({{A}_{1}}\cup {{A}_{2}}\cup {{A}_{3}}\).
- C. \({{A}_{1}}\overline{{{A}_{2}}}\overline{{{A}_{3}}}\cup \overline{{{A}_{1}}}{{A}_{2}}\overline{{{A}_{3}}}\cup \overline{{{A}_{1}}}\overline{{{A}_{2}}}{{A}_{3}}\).
- D. \(\left( {{A}_{1}}\cup \overline{{{A}_{2}}}\cup \overline{{{A}_{3}}} \right)\left( \overline{{{A}_{1}}}\cup {{A}_{2}}\cup \overline{{{A}_{3}}} \right)\left( \overline{{{A}_{1}}}\cup \overline{{{A}_{2}}}\cup {{A}_{3}} \right)\).
-
- A. \(\frac{12}{216}\).
- B. \(\frac{1}{216}\).
- C. \(\frac{6}{216}\).
- D. \(\frac{3}{216}\).
C├óu 4-10: Mß╗Øi c├Īc em ─æ─āng nhß║Łp xem tiß║┐p nß╗Öi dung v├Ā thi thß╗Ł Online ─æß╗ā cß╗¦ng cß╗æ kiß║┐n thß╗®c vß╗ü b├Āi hß╗Źc n├Āy nh├®!
3.2. B├Āi tß║Łp SGK B├Āi 1 To├Īn 11 Ch├ón Trß╗Øi S├Īng Tß║Īo
C├Īc em c├│ thß╗ā xem th├¬m phß║¦n hŲ░ß╗øng dß║½n Giß║Żi b├Āi tß║Łp To├Īn 11 Ch├ón trß╗Øi s├Īng tß║Īo ChŲ░ŲĪng 9 B├Āi 1 ─æß╗ā gi├║p c├Īc em nß║»m vß╗»ng b├Āi hß╗Źc v├Ā c├Īc phŲ░ŲĪng ph├Īp giß║Żi b├Āi tß║Łp.
Hoß║Īt ─æß╗Öng khß╗¤i ─æß╗Öng trang 89 SGK To├Īn 11 Ch├ón trß╗Øi s├Īng tß║Īo tß║Łp 2 - CTST
Hoß║Īt ─æß╗Öng kh├Īm ph├Ī 1 trang 89 SGK To├Īn 11 Ch├ón trß╗Øi s├Īng tß║Īo tß║Łp 2 - CTST
Thß╗▒c h├Ānh 1 trang 89 SGK To├Īn 11 Ch├ón trß╗Øi s├Īng tß║Īo tß║Łp 2 - CTST
Thß╗▒c h├Ānh 2 trang 89 SGK To├Īn 11 Ch├ón trß╗Øi s├Īng tß║Īo tß║Łp 2 - CTST
Thß╗▒c h├Ānh 3 trang 90 SGK To├Īn 11 Ch├ón trß╗Øi s├Īng tß║Īo tß║Łp 2 - CTST
Hoß║Īt ─æß╗Öng kh├Īm ph├Ī 3 trang 90 SGK To├Īn 11 Ch├ón trß╗Øi s├Īng tß║Īo tß║Łp 2 - CTST
Thß╗▒c h├Ānh 4 trang 90 SGK To├Īn 11 Ch├ón trß╗Øi s├Īng tß║Īo tß║Łp 2 - CTST
Hoß║Īt ─æß╗Öng kh├Īm ph├Ī 4 trang 91 SGK To├Īn 11 Ch├ón trß╗Øi s├Īng tß║Īo tß║Łp 2 - CTST
Thß╗▒c h├Ānh 5 trang 92 SGK To├Īn 11 Ch├ón trß╗Øi s├Īng tß║Īo tß║Łp 2 - CTST
Giß║Żi B├Āi 1 trang 93 SGK To├Īn 11 Ch├ón trß╗Øi s├Īng tß║Īo tß║Łp 2 - CTST
Giß║Żi B├Āi 2 trang 93 SGK To├Īn 11 Ch├ón trß╗Øi s├Īng tß║Īo tß║Łp 2 - CTST
Giß║Żi B├Āi 3 trang 93 SGK To├Īn 11 Ch├ón trß╗Øi s├Īng tß║Īo tß║Łp 2 - CTST
Giß║Żi B├Āi 4 trang 93 SGK To├Īn 11 Ch├ón trß╗Øi s├Īng tß║Īo tß║Łp 2 - CTST
Giß║Żi B├Āi 5 trang 93 SGK To├Īn 11 Ch├ón trß╗Øi s├Īng tß║Īo tß║Łp 2 - CTST
B├Āi tß║Łp 1 trang 95 SBT Toa╠ün 11 T├ó╠Żp 2 Ch├ón trß╗Øi s├Īng tß║Īo - CTST
B├Āi tß║Łp 2 trang 95 SBT Toa╠ün 11 T├ó╠Żp 2 Ch├ón trß╗Øi s├Īng tß║Īo - CTST
B├Āi tß║Łp 3 trang 96 SBT Toa╠ün 11 T├ó╠Żp 2 Ch├ón trß╗Øi s├Īng tß║Īo - CTST
B├Āi tß║Łp 4 trang 96 SBT Toa╠ün 11 T├ó╠Żp 2 Ch├ón trß╗Øi s├Īng tß║Īo - CTST
B├Āi tß║Łp 5 trang 96 SBT Toa╠ün 11 T├ó╠Żp 2 Ch├ón trß╗Øi s├Īng tß║Īo - CTST
Hß╗Åi ─æ├Īp B├Āi 1 To├Īn 11 Ch├ón Trß╗Øi S├Īng Tß║Īo
Trong qu├Ī tr├¼nh hß╗Źc tß║Łp nß║┐u c├│ thß║»c mß║»c hay cß║¦n trß╗Ż gi├║p g├¼ th├¼ c├Īc em h├Ży comment ß╗¤ mß╗źc Hß╗Åi ─æ├Īp, Cß╗Öng ─æß╗ōng To├Īn hß╗Źc HOC247 sß║Į hß╗Ś trß╗Ż cho c├Īc em mß╗Öt c├Īch nhanh ch├│ng!
Ch├║c c├Īc em hß╗Źc tß║Łp tß╗æt v├Ā lu├┤n ─æß║Īt th├Ānh t├Łch cao trong hß╗Źc tß║Łp!
-- Mod To├Īn Hß╗Źc 11 Hß╗īC247








