Hoạt động 4 trang 90 SGK Toán 10 Cánh diều tập 2
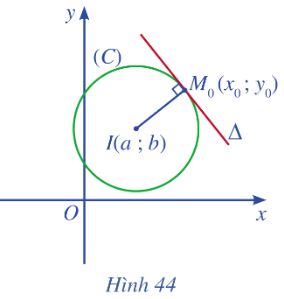
Cho điểm (\({M_o}\left( {{x_o};{\rm{ }}{y_o}} \right)\)) nằm trên đường tròn (C) tâm I(a; b) bán kính R. Gọi \(\Delta \) là tiếp tuyến tại điểm \({M_o}\left( {{x_o};{\rm{ }}{y_o}} \right)\) thuộc đường tròn (Hình 44).
a) Chứng tỏ rằng \(\overrightarrow {I{M_o}} \) là vectơ pháp tuyến của đường thẳng \(\Delta \).
b) Tính toạ độ của \(\overrightarrow {I{M_o}} \).
c) Lập phương trình tổng quát của đường thẳng \(\Delta \).
Hướng dẫn giải chi tiết Hoạt động 4
Phương pháp giải
Phương trình tiếp tuyến của đường tròn tâm I(a, b) tại điểm \({M_0}\left( {{x_0};{y_0}} \right)\) nằm trên đường tròn là:
\(\left( {a - {x_0}} \right)\left( {x - {x_0}} \right) + \left( {b - {y_0}} \right)\left( {y - {y_0}} \right) = 0\)
Hướng dẫn giải
a) Do \(\Delta \) là pháp tuyến của đường tròn (C) tại điểm \({M_o}\) nên \(\Delta \) vuông góc với \(I{M_o}\). Vậy \(\overrightarrow {I{M_o}} \) là vectơ pháp tuyến của đường thẳng \(\Delta \).
b) Tọa độ \(\overrightarrow {I{M_o}} = \left( {{x_o} - a;{y_o} - b} \right)\)
c) Đường thẳng \(\Delta \)đi qua điểm \({M_o}\)và có vecto pháp tuyến \(\overrightarrow {I{M_o}} \)là: \(\left( {{x_o} - a} \right)\left( {x - {x_o}} \right) + \left( {{y_o} - b} \right)\left( {y - {y_o}} \right) = 0\)
-- Mod Toán 10 HỌC247
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.
Bài tập SGK khác
Luyện tập 2 trang 89 SGK Toán 10 Cánh diều tập 2 - CD
Luyện tập 3 trang 89 SGK Toán 10 Cánh diều tập 2 - CD
Luyện tập 4 trang 90 SGK Toán 10 Cánh diều tập 2 - CD
Giải bài 1 trang 91 SGK Toán 10 Cánh diều tập 2 - CD
Giải bài 2 trang 91 SGK Toán 10 Cánh diều tập 2 - CD
Giải bài 3 trang 91 SGK Toán 10 Cánh diều tập 2 - CD
Giải bài 4 trang 92 SGK Toán 10 Cánh diều tập 2 - CD
Giải bài 5 trang 92 SGK Toán 10 Cánh diều tập 2 - CD
Giải bài 6 trang 92 SGK Toán 10 Cánh diều tập 2 - CD
Giải bài 7 trang 92 SGK Toán 10 Cánh diều tập 2 - CD
Giải bài 47 trang 88 SBT Toán 10 Cánh diều tập 2 - CD
Giải bài 48 trang 88 SBT Toán 10 Cánh diều tập 2 - CD
Giải bài 49 trang 88 SBT Toán 10 Cánh diều tập 2 - CD
Giải bài 50 trang 89 SBT Toán 10 Cánh diều tập 2 - CD
Giải bài 51 trang 89 SBT Toán 10 Cánh diều tập 2 - CD
Giải bài 52 trang 89 SBT Toán 10 Cánh diều tập 2 - CD
Giải bài 53 trang 89 SBT Toán 10 Cánh diều tập 2 - CD
Giải bài 54 trang 89 SBT Toán 10 Cánh diều tập 2 - CD
Giải bài 55 trang 89 SBT Toán 10 Cánh diều tập 2 - CD
Giải bài 56 trang 89 SBT Toán 10 Cánh diều tập 2 - CD