Giải bài 41 trang 93 SBT Toán 10 Cánh diều tập 1
Cho hai vectơ \(\overrightarrow a ,\overrightarrow b \) khác vectơ \(\overrightarrow 0 \). Chứng minh rằng nếu hai vectơ cùng hướng thì \(\left| {\overrightarrow a } \right| + \left| {\overrightarrow b } \right| = \left| {\overrightarrow a + \overrightarrow b } \right|\)
Hướng dẫn giải chi tiết Bài 41
Phương pháp giải
Bước 1: Dựng 2 vectơ \(\overrightarrow {AB} = \overrightarrow a ,\overrightarrow {BC} = \overrightarrow b \) thỏa mãn \(\overrightarrow {AB} ,\overrightarrow {BC} \)cùng hướng
Bước 2: Sử dụng quy tắc cộng vectơ và độ dài vectơ để biến đổi giả thiết \(\left| {\overrightarrow a } \right| + \left| {\overrightarrow b } \right| = \left| {\overrightarrow a + \overrightarrow b } \right|\)
Lời giải chi tiết
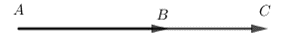
Lấy một điểm A trên mặt phẳng. Dựng \(\overrightarrow {AB} = \overrightarrow a ,\overrightarrow {BC} = \overrightarrow b \) sao cho \(\overrightarrow {AB} ,\overrightarrow {BC} \)cùng hướng
\( \Rightarrow \left| {\overrightarrow a } \right| = AB,\left| {\overrightarrow b } \right| = BC\)
Ta có: \(\overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \Leftrightarrow \overrightarrow a + \overrightarrow b = \overrightarrow {AC} \)
Lại có: AB + BC = AC \( \Rightarrow \left| {\overrightarrow a } \right| + \left| {\overrightarrow b } \right| = AC = \left| {\overrightarrow {AC} } \right| = \left| {\overrightarrow a + \overrightarrow b } \right|\) (ĐPCM)
-- Mod Toán 10 HỌC247
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.
Bài tập SGK khác
Giải bài 39 trang 92 SBT Toán 10 Cánh diều tập 1 - CD
Giải bài 40 trang 92 SBT Toán 10 Cánh diều tập 1 - CD
Giải bài 42 trang 93 SBT Toán 10 Cánh diều tập 1 - CD
Giải bài 43 trang 93 SBT Toán 10 Cánh diều tập 1 - CD
Giải bài 44 trang 93 SBT Toán 10 Cánh diều tập 1 - CD





