Giải bài 29 trang 85 SBT Toán 10 Cánh diều tập 1 - CD

Phương pháp giải

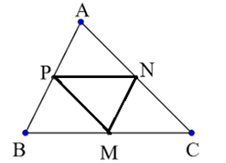
Bước 1: Chứng minh MNAP là hình bình hành rồi suy ra \(\overrightarrow {MN}  = \overrightarrow {PA} \)

Bước 2: Chứng minh MPNC là hình bình hành rồi suy ra \(\overrightarrow {MP}  = \overrightarrow {CN} \)

Lời giải chi tiết

a) Theo giả thiết, MN là đường trung bình của tam giác ABC \( \Rightarrow MN//AB,MN = \frac{1}{2}AB\)

mà P là trung điểm AB nên \(MN//AP,MN = AP\)

Do đó MNAP là hình bình hành \( \Rightarrow \)\(\overrightarrow {MN}  = \overrightarrow {PA} \)

a) Theo giả thiết, MP là đường trung bình của tam giác ABC \( \Rightarrow MP//AC,MP = \frac{1}{2}AC\)

mà N là trung điểm AC nên \(MP//AN,MP = AN\)

Do đó MPNC là hình bình hành \( \Rightarrow \)\(\overrightarrow {MP}  = \overrightarrow {CN} \)

-- Mod Toán 10 HỌC247