Giải bài 2 trang 13 SBT Toán 10 Chân trời sáng tạo tập 2
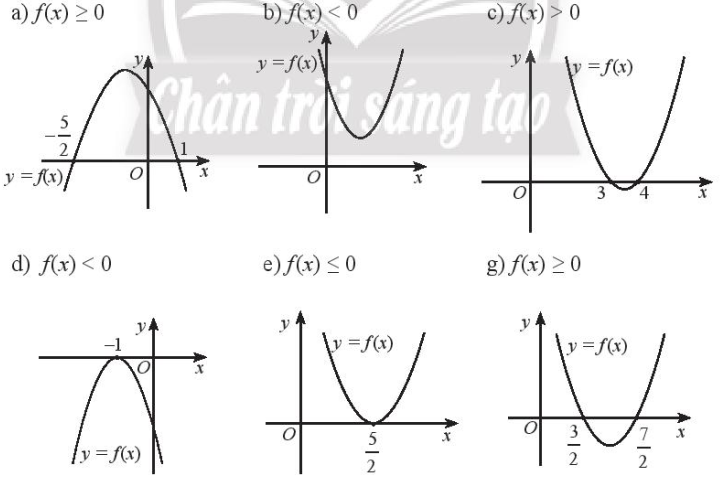
Dựa vào đồ thị của hàm số bậc hai đã cho, hãy nêu tập nghiệm của các bất phương trình bậc hai tương ứng
Hướng dẫn giải chi tiết Bài 2
Phương pháp giải
a) Phần đồ thị nằm trên trục hoành tương ứng với \(x \in \left( { - \frac{5}{2};1} \right)\)
b) Dễ thấy toàn bộ đồ thị đều nằm phía trên trục hoành, do đó \(f\left( x \right) > 0\) với mọi \(x \in \mathbb{R}\). Vậy tập nghiệm của bất phương trình \(f\left( x \right) < 0\) là \(\emptyset \)
c) Phần đồ thị nằm trên trục hoành tương ứng với \(x \in \mathbb{R}{\rm{\backslash }}\left( {3;4} \right)\)
d) Dễ thấy đồ thị nằm phía dưới trục hoành và cắt trục hoành tại (-1;0)
e) Dễ thấy đồ thị nằm phía trên trục hoành và cắt trục hoành tại \(\left( {\frac{5}{2};0} \right)\)
g) Phần đồ thị nằm trên trục hoành tương ứng với \(x \in \left( { - \infty ;\frac{3}{2}} \right) \cup \left( {\frac{7}{2}; + \infty } \right)\)
Lời giải chi tiết
a) Phần đồ thị nằm trên trục hoành tương ứng với \(x \in \left( { - \frac{5}{2};1} \right)\)
Do đó \(f\left( x \right) \ge 0\) khi và chỉ khi \( - \frac{5}{2} \le x \le 1\)
Vậy tập nghiệm của bất phương trình \(f\left( x \right) \ge 0\) là \(\left[ { - \frac{5}{2};1} \right]\)
b) Dễ thấy toàn bộ đồ thị đều nằm phía trên trục hoành, do đó \(f\left( x \right) > 0\) với mọi \(x \in \mathbb{R}\). Vậy tập nghiệm của bất phương trình \(f\left( x \right) < 0\) là \(\emptyset \)
c) Phần đồ thị nằm trên trục hoành tương ứng với \(x \in \mathbb{R}{\rm{\backslash }}\left( {3;4} \right)\)
Do đó\(f\left( x \right) > 0\) khi và chỉ khi \(x < 3\) hoặc \(x > 4\)
Vậy tập nghiệm của bất phương trình \(f\left( x \right) > 0\) là \(\left( { - \infty ;3} \right) \cup \left( {4; + \infty } \right)\)
d) Dễ thấy đồ thị nằm phía dưới trục hoành và cắt trục hoành tại (-1;0)
Do đó \(f\left( x \right) < 0\) khi và chỉ khi \(x \ne - 1\)
Vậy tập nghiệm của bất phương trình \(f\left( x \right) < 0\) là \(\mathbb{R}\backslash \left\{ { - 1} \right\}\)
e) Dễ thấy đồ thị nằm phía trên trục hoành và cắt trục hoành tại \(\left( {\frac{5}{2};0} \right)\)
Do đó \(f\left( x \right) > 0\) với mọi \(x \ne \frac{5}{2}\) và \(f(x) = 0\) tại \(x = \frac{5}{2}\)
Suy ra \(f\left( x \right) \le 0 \Leftrightarrow f(x) = 0 \Leftrightarrow x = \frac{5}{2}\)
Vậy tập nghiệm của bất phương trình \(f\left( x \right) \le 0\) là \(\left\{ {\frac{5}{2}} \right\}\)
g) Phần đồ thị nằm trên trục hoành tương ứng với \(x \in \left( { - \infty ;\frac{3}{2}} \right) \cup \left( {\frac{7}{2}; + \infty } \right)\)
\(f\left( x \right) = 0\) khi và chỉ khi \(x = \frac{3}{2}\) hoặc \(x = \frac{7}{2}\)
Vậy tập nghiệm của bất phương trình \(f\left( x \right) \ge 0\) là \(\left( { - \infty ;\frac{3}{2}} \right] \cup \left[ {\frac{7}{2}; + \infty } \right)\)
-- Mod Toán 10 HỌC247
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.
Bài tập SGK khác
Giải bài 5 trang 13 SGK Toán 10 Chân trời sáng tạo tập 2 - CTST
Giải bài 1 trang 13 SBT Toán 10 Chân trời sáng tạo tập 2 - CTST
Giải bài 3 trang 14 SBT Toán 10 Chân trời sáng tạo tập 2 - CTST
Giải bài 4 trang 14 SBT Toán 10 Chân trời sáng tạo tập 2 - CTST
Giải bài 5 trang 14 SBT Toán 10 Chân trời sáng tạo tập 2 - CTST
Giải bài 6 trang 14 SBT Toán 10 Chân trời sáng tạo tập 2 - CTST
Giải bài 7 trang 14 SBT Toán 10 Chân trời sáng tạo tập 2 - CTST
Giải bài 8 trang 14 SBT Toán 10 Chân trời sáng tạo tập 2 - CTST
Giải bài 9 trang 15 SBT Toán 10 Chân trời sáng tạo tập 2 - CTST
Giải bài 10 trang 15 SBT Toán 10 Chân trời sáng tạo tập 2 - CTST
Giải bài 11 trang 15 SBT Toán 10 Chân trời sáng tạo tập 2 - CTST
Giải bài 12 trang 15 SBT Toán 10 Chân trời sáng tạo tập 2 - CTST





