Giải bài 2.17 trang 25 SBT Toán 10 Kết nối tri thức tập 1
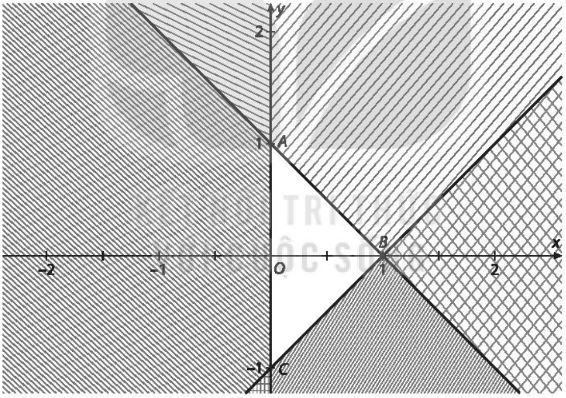
Miền nghiệm của hệ bất phương trình nào dưới đây là miền tam giác \(ABC\) (miền không bị gạch)?
A. \(\left\{ {\begin{array}{*{20}{c}}{x + y \le 1}\\{x - y \ge 1}\\{x \ge 0}\end{array}.} \right.\)
B. \(\left\{ {\begin{array}{*{20}{c}}{x + y \le 1}\\{x - y \le 1}\\{x \ge 0}\end{array}} \right..\)
C. \(\left\{ {\begin{array}{*{20}{c}}{x - y \ge - 1}\\{x + y \ge - 1}\\{x \ge 0}\end{array}.} \right.\)
D. \(\left\{ {\begin{array}{*{20}{c}}{x - y \ge - 1}\\{x + y \ge - 1}\\{y \ge 0}\end{array}.} \right.\)
Hướng dẫn giải chi tiết Bài 2.17
Phương pháp giải
- Hệ bất phương trình bậc nhát hai ần là một hệ gồm hai hay nhiều bắt phương trình bậc nhất hai ẩn.
- Cặp số (x0; y0) là nghiệm của một hệ bất phương trình bậc nhất hai ẩn khi (x0; y0) đồng thời là nghiệm của tất cả các bất phương trình trong hệ đó.
Lời giải chi tiết
Dễ thấy đáp án D sai.
Thay điểm \(O\left( {0;0} \right)\) vào bất phương trình, \(x - y \ge 1\)ta được:
\(0 - 0 = 0 > 1\) (vô lý)
\( \Rightarrow \) loại đáp án A.
Thay điểm \(O\left( {0;0} \right)\) vào bất phương trình, \(\left\{ {\begin{array}{*{20}{c}}{x + y \le 1}\\{x - y \le 1}\\{x \ge 0}\end{array}} \right.\) ta được:
\(\left\{ {\begin{array}{*{20}{c}}{0 + 0 = 0 < 1}\\{0 - 0 < 1}\\{0 \ge 0}\end{array}} \right.\) (thỏa mãn)
\( \Rightarrow \) đáp án B đúng.
Chọn B.
-- Mod Toán 10 HỌC247
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.
Bài tập SGK khác
Giải bài 2.15 trang 25 SBT Toán 10 Kết nối tri thức tập 1 - KNTT
Giải bài 2.16 trang 25 SBT Toán 10 Kết nối tri thức tập 1 - KNTT
Giải bài 2.18 trang 26 SBT Toán 10 Kết nối tri thức tập 1 - KNTT
Giải bài 2.19 trang 26 SBT Toán 10 Kết nối tri thức tập 1 - KNTT
Giải bài 2.20 trang 26 SBT Toán 10 Kết nối tri thức tập 1 - KNTT
Giải bài 2.21 trang 26 SBT Toán 10 Kết nối tri thức tập 1 - KNTT
Giải bài 2.22 trang 26 SBT Toán 10 Kết nối tri thức tập 1 - KNTT
Giải bài 2.23 trang 26 SBT Toán 10 Kết nối tri thức tập 1 - KNTT
Giải bài 2.24 trang 27 SBT Toán 10 Kết nối tri thức tập 1 - KNTT
Giải bài 2.25 trang 27 SBT Toán 10 Kết nối tri thức tập 1 - KNTT
Giải bài 2.26 trang 27 SBT Toán 10 Kết nối tri thức tập 1 - KNTT
Giải bài 2.27 trang 27 SBT Toán 10 Kết nối tri thức tập 1 - KNTT
Giải bài 2.28 trang 27 SBT Toán 10 Kết nối tri thức tập 1 - KNTT
Giải bài 2.29 trang 28 SBT Toán 10 Kết nối tri thức tập 1 - KNTT