Sau đây mời các em học sinh lớp 10 cùng tham khảo bài Các số đặc trưng đo xu thế trung tâm. Bài giảng đã được soạn khái quát lý thuyết cần nhớ, đồng thời có các bài tập minh họa có lời giải chi tiết giúp các em dễ dàng nắm được kiến thức trọng tâm của bài.
Tóm tắt lý thuyết
1.1. Số trung bình và trung vị
a. Số trung bình
| Số trung bình (số trung bình cộng) của mẫu số liệu \({x_1},{x_2},{x_3},...,{x_n}\), kí hiệu là \(\overline x \) được tính bằng công thức: \(\overline x = \frac{{{x_1} + {x_2} + {x_3} + ... + {x_n}}}{n}\) |
|---|
Chú ý: Trong trường hợp số liệu cho dưới dạng bảng tần số thì số trung bình được tính theo công thức: \(\bar x = \frac{{{m_1}{x_1} + {m_2}{x_2} + ... + {m_k}{x_k}}}{n}\)
Trong đó \({m_k}\) là tần số của giá trị \({x_k}\) và \(n = {m_1} + {m_2} + ... + {m_k}\)
Ý nghĩa: Số trung bình là giá trị trung bình cộng của các số trong mẫu số liệu, nó cho biết vị trí trung tâm của mẫu số liệu và có thể dùng để đại diện cho mẫu số liệu.
Ví dụ: Thống kê số cuốn sách mỗi bạn trong lớp đã đọc trong năm 2021, An thu được kết quả như bảng bên. Hỏi trong năm 2021, trung bình mỗi bạn trong lớp đọc bao nhiêu cuốn sách?
Giải
Số bạn trong lớp là n = 3 + 5 + 15 + 10 + 7 = 40 (bạn).
Trong năm 2021, trung bình mỗi bạn trong lớp đọc số cuốn sách là:
\(\frac{{3.1 + 5.2 + 15.3 + 10.4 + 7.5}}{{40}} = 3,325\) (cuốn).
b. Trung vị
|
Để tìm trung vị của một mẫu số liệu, ta thực hiện như sau: + Sắp xếp các giá trị trong mẫu số liệu theo thứ tự không giảm. + Nếu số giá trị của mẫu số liệu là số lẻ thì giá trị chinh giữa của mẫu là trung vị. Nếu là số chẵn thì trung vị là trung bình cộng của hai giá trị chính giữa của mẫu. |
|---|
Ý nghĩa: Trung vị là giá trị chia đôi mẫu só liệu, nghĩa là trong mẫu số liệu được sắp xếp theo thứ tự không giảm thì giá trị trung vị ở vị trí chính giữa. Trung vị không bị ảnh hưởng bởi giá trị bất thường trong khi số trung bình bị ảnh hưởng bởi giá trị bất thường.
Ví dụ: Một công ty nhỏ gồm 1 giám đốc và 5 nhân viên, thu nhập mỗi tháng của giám đốc là 20 triệu đồng, của nhân viên là 4 triệu đồng. Hãy tìm trung vị cho mẫu số liệu vẻ lương của giám đóc và nhân viên công ty.
Giải
Đề tim trung vị của mẫu số liệu trên, ta làm như sau:
+ Sắp xếp số liệu theo thứ tự không giảm
+ Dãy trên có hai giá trị chính giữa cùng bằng 4. Vậy trung vị của mẫu số liệu cũng bằng 4. Trong mẫu số liệu được sắp xếp trên, số phần tử ở bên trái trung vị và số phần tử ở bên phải trung vị bằng nhau và bằng 3. Lương của giám đốc cao hơn hẳn số trung bình, đây chính là
giá trị bất thường. Nễu ta thay lương của giám đốc là 30; 40; 50... (triệu đồng) thì trung vị vẫn không thay đổi trong khi số trung bình sẽ thay đổi.
1.2. Tứ phân vị
|
Để tìm các tứ phân vị của mẫu số liệu có n giá trị, ta làm như sau: + Sắp xếp mẫu số liệu theo thứ tự không giảm. + Tìm trung vị. Giá trị này là Q2. + Tìm trung vị của nừa số liệu bên trái Q2, (không bao gồm Q2, nếu n lẻ). Giá trị nảy là Q1. + Tim trung vị của nửa số liệu bên phải Q2, (không bao gồm Q2, nếu n lẻ). Giá trị này là Q3. Q1, Q2, Q3 được gợi là các tử phân vị của mẫu số liệu. |
|---|
Chú ý: Q1 được gọi là tứ phân vị thứ nhất hay tứ phân vị dưới, Q3 được gọi là tứ phân vị thứ ba hay tứ phân vị trên.
Ý nghĩa: Các điểm Q1, Q2, Q3 chia mẫu số liệu đã sắp xếp theo thứ tự từ nhỏ đến lớn thành bốn phần, mỗi phần đều chứa 25% giá trị.
Ví dụ: Hàm lượng Natri (đơn vị miligam, 1 mg = 0,001 g) trong 100 g một số loại ngũ cóc được cho như sau:
Hãy tìm các tứ phân vị. Các tứ phân vị này cho ta thông tin gi?
Giải
+ Sắp xếp các giá trị này theo thứ tự không giảm:
+ Vì n= 20 là số chẵn nên Q2 là trung bình cộng của hai giá trị chính giữa:
Q2 = (180 + 180) : 2 = 180.
+ Ta tìm Q1 là trung vị của nủa số liệu bên trái Q2:
Và tìm được Q1 = (130 + 140) : 2 = 135.
+ Ta tìm Q3 là trung vị của nửa số liệu bên phải Q2:
và tìm được Q3 = (200 + 210) : 2 = 205
Hình ảnh về sự phân bố của mẫu số liệu
Các tứ phân vị cho ta hình ảnh phân bỗ của mẫu số liệu. Khoảng cách từ Q1 đến Q2 là 45 trong khi khoảng cách từ Q2 đền Q3 là 25. Điều này cho thấy mẫu số liệu tập trung với mật độ cao ở bên phải của Q2 và mật độ thấp ở bên trái của Q2.
1.3. Mốt
| Mốt của mẫu số liệu là giá trị xuất hiện với tần số lớn nhất. |
|---|
Ý nghĩa: Dùng mốt để đo xu thế trung tâm của mẫu số liệu khi mẫu có nhiều giá trị trùng nhau.
Ví dụ: Thời gian truy cập Internet (đơn vị giờ) trong một ngày của một số học sinh lớp 10 được cho như sau:
Tìm mốt cho mẫu số liệu này.
Giải
Vì số học sinh truy cập Intemet 1 giờ mỗi ngày là lớn nhất (có 3 học sinh) nên mốt là 1.
Nhận xét
+ Mốt có thẻ không là duy nhất. Chẳng hạn, với mẫu số liệu
các số 7; 8 đều xuất hiện với số lần lớn nhất (3 lần) nên mẫu số liệu này có hai mốt là 7 và 8.
+ Khi các giá tị trong mấu số liệu xuất hiện với tần số như nhau thì mẫu số liệu không có mốt.
+ Mốt còn được định nghĩa cho mẫu dữ liệu định tính (dữ liệu không phải là số). Ví dụ báo Tuổi trẻ đã thực hiện thăm dò ý kiến của bạn đọc với câu hỏi "Theo bạn, VFF nên chọn huấn luyện viên ngoại hay nội dẫn dắt đội tuyển bóng đá nam Việt Nam?".
Tại thời điểm 21 giờ ngày 27-4-2021 kết quả bình chọn như sau:
Trong mẫu dữ liệu này, lựa chọn "huấn luyện viên ngoại" có nhiều người bình chọn nhất, được gọi là mốt.
Bài tập minh họa
Câu 1: Chiều dài (đơn vị feet) của 7 con cá voi trưởng thành được cho như sau:
48 53 51 31 53 112 52
Tìm số trung bình và trung vị của mẫu số liệu trên. Trong hai số đó, số nào phù hợp hơn để đại diện cho chiều dài của 7 con cá voi trưởng thành này?
Hướng dẫn giải
Số trung bình: \(\bar X = \frac{{48 + 53 + 51 + 31 + 53 + 112 + 52}}{7}\)\( = \frac{{400}}{7} \approx 57,14\)
Số trung vị:
Ta sắp xếp lại số liệu theo thứ tự không giảm:
31 48 51 52 53 53 112
Số giá trị là 7, là số lẻ nên giá trị chính giữa của mẫu là trung vị. Mà giá trị chính giữa là 52.
Vậy số trung vị là 52.
Ta thấy trong mẫu số liệu bài cho thì 112 cao hơn hẳn giá trị trung bình nên không thể dùng số trung bình để đại diện cho chiều dài của 7 con cá voi trưởng thành này.
Vậy ta dùng số trung vị để đại diện cho chiều dài của 7 con cá voi trưởng thành này.
Câu 2: Bảng sau đây cho biết số lần học tiếng Anh trên internet trong một tuần của một số học sinh lớp 10:
|
Số lần |
0 |
1 |
2 |
3 |
4 |
5 |
|
Số học sinh |
2 |
4 |
6 |
12 |
8 |
3 |
Hãy tìm các tứ phân vị cho mẫu số liệu này.
Hướng dãn giải
Ta thấy n=2+4+6+12+8+3=35.
Trung vị là học sinh thứ 18
Ta thấy 2+4+6<18<2+4+6+12
=> \({Q_2} = 3\)
Ta tìm \({Q_1}\) là trung vị của nửa số liệu bên trái \({Q_2}\)(không bao gồm \({Q_2}\))
Nửa số liệu bên trái \({Q_2}\) có 17 học sinh nên trung vị là học sinh thứ 9:
Ta thấy 2+4<9<2+4+6
=>\({Q_1} = 2\)
Ta tìm \({Q_3}\) là trung vị của nửa số liệu bên phải \({Q_2}\)(không bao gồm \({Q_2}\))
Nửa số liệu bên phải \({Q_2}\) có 17 học sinh nên trung vị là học sinh thứ 9 trong 17 học sinh và là học sinh thứ 9+18=27 trong 35 học sinh.
Ta thấy 2+4+6+12<27<2+4+6+12+8
=>\({Q_3} = 4\)
Luyện tập Bài 13 Toán 10 KNTT
Qua bài giảng trên sẽ giúp các em nắm được các nội dung như sau:
- Khái niệm trung bình cộng của một dãy số liệu thống kê.
- Số trung vị, mốt và ý nghĩa của nó.
3.1. Bài tập trắc nghiệm Bài 13 Toán 10 KNTT
Để cũng cố bài học xin mời các em cũng làm Bài kiểm tra Trắc nghiệm Toán 10 Kết nối tri thức Chương 5 Bài 13 để kiểm tra xem mình đã nắm được nội dung bài học hay chưa.
-
- A. Trong 40 số liệu thống kê trên, số giá trị khác nhau là 8
- B. M0 = 8
- C. Me = 6,5
- D. Giá trị trung bình là: \(\bar X \approx 6,67\)
-
- A. 31,5
- B. 32
- C. 32,5
- D. 33
-
- A. 6,9
- B. 7,0
- C. 6,8
- D. 8,6
Câu 4-10: Mời các em đăng nhập xem tiếp nội dung và thi thử Online để củng cố kiến thức và nắm vững hơn về bài học này nhé!
3.2. Bài tập SGK Bài 13 Toán 10 KNTT
Bên cạnh đó các em có thể xem phần hướng dẫn Giải bài tập Toán 10 Kết nối tri thức Chương 5 Bài 13 để giúp các em nắm vững bài học và các phương pháp giải bài tập.
Hoạt động 1 trang 78 SGK Toán 10 Kết nối tri thức tập 1 - KNTT
Hoạt động 2 trang 78 SGK Toán 10 Kết nối tri thức tập 1 - KNTT
Luyện tập 1 trang 79 SGK Toán 10 Kết nối tri thức tập 1 - KNTT
Hoạt động 3 trang 79 SGK Toán 10 Kết nối tri thức tập 1 - KNTT
Luyện tập 2 trang 79 SGK Toán 10 Kết nối tri thức tập 1 - KNTT
Hoạt động 4 trang 80 SGK Toán 10 Kết nối tri thức tập 1 - KNTT
Luyện tập 3 trang 81 SGK Toán 10 Kết nối tri thức tập 1 - KNTT
Hoạt động 5 trang 81 SGK Toán 10 Kết nối tri thức tập 1 - KNTT
Vận dụng trang 82 SGK Toán 10 Kết nối tri thức tập 1 - KNTT
Giải bài 5.7 trang 82 SGK Toán 10 Kết nối tri thức tập 1 - KNTT
Giải bài 5.8 trang 82 SGK Toán 10 Kết nối tri thức tập 1 - KNTT
Giải bài 5.9 trang 83 SGK Toán 10 Kết nối tri thức tập 1 - KNTT
Giải bài 5.10 trang 83 SGK Toán 10 Kết nối tri thức tập 1 - KNTT
Giải bài 5.7 trang 76 SBT Toán 10 Kết nối tri thức tập 1 - KNTT
Giải bài 5.8 trang 76 SBT Toán 10 Kết nối tri thức tập 1 - KNTT
Giải bài 5.9 trang 77 SBT Toán 10 Kết nối tri thức tập 1 - KNTT
Giải bài 5.10 trang 77 SBT Toán 10 Kết nối tri thức tập 1 - KNTT
Giải bài 5.11 trang 77 SBT Toán 10 Kết nối tri thức tập 1 - KNTT
Giải bài 5.12 trang 77 SBT Toán 10 Kết nối tri thức tập 1 - KNTT
Hỏi đáp Bài 13 Toán 10 KNTT
Trong quá trình học tập nếu có thắc mắc hay cần trợ giúp gì thì các em hãy comment ở mục Hỏi đáp, Cộng đồng Toán HOC247 sẽ hỗ trợ cho các em một cách nhanh chóng!
Chúc các em học tập tốt và luôn đạt thành tích cao trong học tập!
-- Mod Toán Học 10 HỌC247


.JPG)

.JPG)
.JPG)
.JPG)
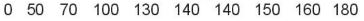
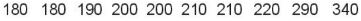

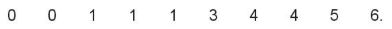


.JPG)
.JPG)
.JPG)





