Bạn bè (0)
Hoạt động gần đây (54)
-
hồ Thư đã trả lời trong câu hỏi: Cho hai số a và b thỏa mãn a cộng b bằng 4 .Chứng minh rằng ab nhỏ hơn hoặc bằng 4 Cách đây 7 năm
nếu a,b >hoặc =0 thì bạn mới được sử dụng BĐTcôsi như các bạn ở trên vì coossi chỉ áp dụng với các số 0 âm
-
hồ Thư đã trả lời trong câu hỏi: cân bằng phương trình phức tạp Cách đây 7 năm
17Al+72HNO3=>17Al(NO3)3+15NO+6NO2+36H2O
-
hồ Thư đã trả lời trong câu hỏi: cân bằng phương trình phức tạp Cách đây 7 năm
25Mg+64HNO3=>25Mg(NO3)2+6NO+4N2O+32H2O
-
hồ Thư đã trả lời trong câu hỏi: toán hoc lớp 12 Cách đây 7 năm
bằng 4 bạn ạ
-
hồ Thư đã đặt câu hỏi: đề thi huyện hóa Cách đây 7 năm
hoa tan hoan toan 17,2 g hon hop A gom Fe và FexOy bang 500g dung dịch H2SO4 9,8% thu được khí hidro co the tich dung bang the tich 3,2 g khi oxy và dung dịch B trong do co 22,8 g FeSO4
a, xác dinh cong thuc FexOy
b, tính C% cua dung dich sau pư
-
hồ Thư đã trả lời trong câu hỏi: Bài 111 trang 94 sách bài tập toán 8 tập 1 Cách đây 7 năm
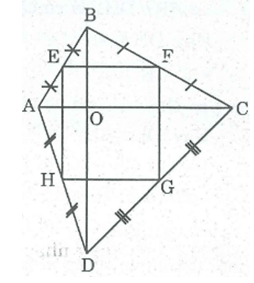
* Trong ΔABC, ta có:
E là trung điểm của AB (gt)
F là trung điểm của BC (gt)
Nên EF là đường trung bình của ΔABC
⇒ EF // AC và EF = 1/2 AC (tính chất đường trung bình tam giác) (1)
* Trong ΔDAC, ta có:
H là trung điểm của AD (gt)
G là trung điểm của DC (gt)
Nên HG là đường trung bình của ΔDAC.
⇒ HG // AC và HG = 1/2 AC (tính chất đường trung bình tam giác) (2)
Từ (1) và (2) suy ra: EF // HG và EF = HG
Suy ra tứ giác EFGH là hình bình hành (vì có một cặp cạnh đối song song và bằng nhau)
Ta lại có: BD ⊥ AC (gt)
EF // AC (chứng minh trên)
Suy ra: EF ⊥ BD
Trong ΔABD ta có EH là đường trung bình ⇒ EH // BD
Suy ra: EF ⊥ EH hay (FEH) = 90o
Vậy hình bình hành EFGH là hình chữ nhật.
-
hồ Thư đã trả lời trong câu hỏi: Bài 110 trang 93 sách bài tập toán 8 tập 1 Cách đây 7 năm
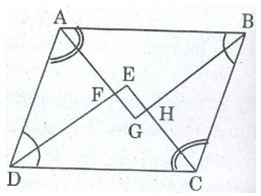
Gọi G, H, E, F lần lượt là giao điểm của các đường phân giác của ∠Avà ∠B; ∠Bvà ∠C; ∠Cvà ∠D; ∠Dvà ∠A
Ta có: ∠(ADF) = 1/2 ∠(ADC) (gt)
∠(DAF) = 1/2 ∠(DAB) (gt)
∠(ADC) + ∠(DAB) = 180o (hai góc trong cùng phía)
Suy ra: ∠(ADF) + ∠(DAF) = 1/2 (∠(ADC) + ∠(DAB) ) = 1/2 .180o = 90o
Trong ΔAFD, ta có:
∠(AFD) = 180o – (∠(ADF) + ∠(DAF)) = 180o – 90o = 90o
∠(EFG) = ∠(AFD) (đối đỉnh)
⇒ ∠(EFG) = 90o
∠(GAB) = 1/2 ∠(DAB) (gt)
∠(GBA) = 1/2 ∠(CBA) (gt)
∠(DAB) + ∠(CBA) = 180o (hai góc trong cùng phía)
⇒ (GAB) + (GBA) = 1/2 (∠(DAB) + ∠(CBA) ) = 1/2 .180o = 90o
Trong ΔAGB ta có: ∠(AGB) = 180o – (∠(GAB) + ∠(GBA) ) = 1/2 .180o = 90o
Hay ∠G = 90o
∠(EDC) = 1/2 ∠(ADC) (gt)
∠(ECD) = 1/2 ∠(BCD) (gt)
∠(ADC) + ∠(BCD) = 180o (hai góc trong cùng phía)
⇒ ∠(EDC) + ∠(ECD) = 1/2 (∠(ADC) + ∠(BCD) ) = 1/2 .180o = 90o
Trong ΔEDC ta có: ∠(DEC) = 180o – (∠(EDC) + ∠(ECD) ) = 1/2 .180o = 90o
Hay ∠E = 90o
Vậy tứ giác EFGH là hình chữ nhật (vì có ba góc vuông).
-
hồ Thư đã trả lời trong câu hỏi: Bài 92 trang 91 sách bài tập toán 8 tập 1 Cách đây 7 năm
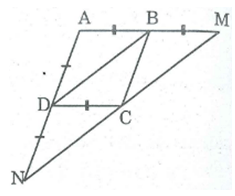
Tứ giác ABCD là hình bình hành:
⇒ AB // CD hay BM // CD
Xét tứ giác BMCD ta có:
BM // CD
BM = CD (gt)
=> Tứ giác BMCD là hình bình hành (vì có một cặp cạnh đối song song và bằng nhau)
⇒ MC // BD và MC = BD (1)
AD // BC (gt) haỵ DN // BC
Xét tứ giác BCND ta có: DN // BC và DN = BC (vì cùng bằng AD)
Suy ra: Tứ giác BCND là hình bình hành (vì có một cặp cạnh đối song song và bằng nhau)
⇒ CN // BD và CN = BD (2)
Từ (1) và (2) suy ra: M, C, N thẳng hàng và MC = CN.
-
hồ Thư đã trả lời trong câu hỏi: Bài 99 trang 92 sách bài tập toán 8 tập 1 Cách đây 7 năm
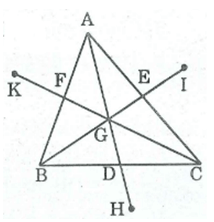
* Ta có: GD = DH (tính chất đối xứng tâm)
⇒ GH = 2GD (l)
GA = 2GD (tính chất đường trung tuyến của tam giác) (2)
Từ (1) và (2) suy ra: GA = GH
Suy ra điểm đối xứng với điểm A qua tâm G là H.
* Ta có: GE = EI (tính chất đối xứng tâm)
⇒ GI = 2GB (3)
GB = 2GE (tính chất đường trung tuyên của tam giác) (4)
Từ (3) và (4) suy ra: GB = GI
Suy ra điểm đối xứng với điểm B qua tâm G là I.
GF = FK (tỉnh chất đối xứng tâm)
⇒ GK = 2GF (5)
GC = 2GF (tính chất đường trung tuyến của tam giác) (6)
Từ (5) và (6) Suy ra: GC = GK
Suy ra điểm đối xứng với điểm C qua tâm G là điểm K
-
hồ Thư đã trả lời trong câu hỏi: Bài 109 trang 93 sách bài tập toán 8 tập 1 Cách đây 7 năm
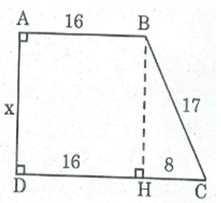
Kẻ BH ⊥ CD,ta có: ∠A = 90o, ∠D = 90o, ∠(BHD) = 90o
Suy ra tứ giác ABHD là hình chữ nhật (vì có ba góc vuông)
⇒ AB = DH, BH = AD
HC = CD – DH = CD – AB = 24 – 16 = 8 (cm)
Trong tam giác vuông BHC, theo định lý Pi-ta-go, ta có:
BC2 = BH2 + HC2
⇒ BH2 = BC2 - HC2
BH2 = l72 - 82 = 289 – 64 = 225
BH = √225 = 15 (cm)
Vậy x = AD = BH = 15 (cm).