-
Câu hỏi:
Một hình lập phương có cạnh bằng 2a vừa nội tiếp hình lăng trụ (T) vừa nội tiếp mặt cầu (C). Tính tỉ số thể tích giữa khối cầu và khối lăng trụ giới hạn bởi (C) và (T)?
- A.
- B.
- C.
- D.
Đáp án đúng: A
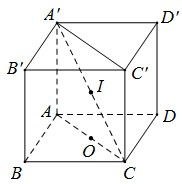
Xét hình trụ , ngoài ra
(1)
Xét mặt cầu
(2)
(1) và (2) suy ra
YOMEDIA
Hướng dẫn Trắc nghiệm Online và Tích lũy điểm thưởng
CÂU HỎI KHÁC VỀ MẶT TRỤ, HÌNH TRỤ, KHỐI TRỤ
- Xác định chiều cao và bán kính để hình trụ nội tiếp hình cầu bán kính bằng 3 có thể tích lớn nhất
- Một hình trụ có hai đáy là hai hình tròn (O;r) và (O';r) OO'=r căn 3 một hình nón có đỉnh là O’ và có đáy là hình tròn (O;r)
- Tính bán kính mặt cầu có diện tích bằng diện tích toàn phần hình trụ tạo thành khi quay hình vuông ABCD quanh MN
- Tính thể tích V của khối trụ có chiều cao bằng 3, chu vi đáy bằng 4pi
- Tính thể tích khối trụ có một đáy thuộc đáy của hình nón và đường tròn đáy của mặt đáy còn lại thuộc mặt xung quanh của hình nón có góc ở đỉnh bằng 900 và bán kính đáy bằng 4
- Tính thể tích V của khối nón có độ dài đường sinh bằng 2a và mặt phẳng qua trục cắt hình nón theo thiết diện là tam giác vuông
- Xếp 7 hình trụ nhỏ vào một lọ hình trụ sao cho hình trụ nằm chính giữa tiếp xúc với sáu hình trụ xung quanh mỗi hình trụ xung quanh đều tiếp xúc với mặt bên hình trụ lớn
- Tính diện tích xung quanh S của hình trụ có diện tích thiết diện qua trục là 25
- Cắt hình trụ có bán kính đáy là R=5(cm), khoảng cách giữa hai đáy là 7(cm) bằng một mặt phẳng song song với trục và cách trục hình trụ một khoảng 3(cm)
- Tính thể tích V của khối trụ tạo thành khi quay hình chữ nhật ABCD có AD = a; AB = 3a một vòng quanh cạnh AD






