Một con lắc đơn dao động điều hòa với chu kì T tại nơi có thêm ngoại lực có độ lớn F theo phương ngang. Nếu quay phương ngoại lực một góc $\alpha$ $\left( {{0^0} < \alpha < {{90}^0}} \right)$ trong mặt phẳng thẳng đứng và giữ nguyên độ lớn thì chu kì dao động là ${T_1} = 2,4{\rm{s}}$ hoặc ${T_2} = 4,8s$. Chu kì T gần giá trị nào nhất sau đây?

Đáp án : A

Con lắc đơn có chu kì dao động: $T = 2\pi \sqrt {\frac{l}{g}}$

$\Rightarrow {T^2} = 4{\pi ^2}.\frac{l}{g} \Rightarrow g \sim \frac{1}{{{T^2}}}$

+ Ban đầu $\overrightarrow F$ theo phương ngang, ta có gia tốc biểu kiến khi này $g' = \sqrt {{g^2} + {a^2}}$

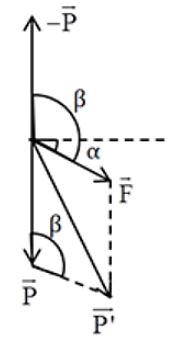
+ Khi $\overrightarrow F$ hướng xuống

Có:$\beta = {90^0} + \alpha \Rightarrow \cos \beta = \sin \alpha$

Gia tốc hiệu dụng khi này: ${g_1} = \sqrt {{g^2} + {a^2} - 2ag\sin \alpha }$

$\Rightarrow g_1^2 = {g^2} + {a^2} - 2ag\sin \alpha \,\,\,\,\left( 1 \right)$

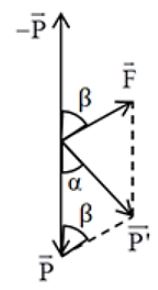
+ Khi $\overrightarrow F$ hướng lên trên

Ta có $\beta = {90^0} - \alpha \Rightarrow co{\rm{s}}\beta = {\rm{ - sin}}\alpha$

Gia tốc hiệu dụng khi này: ${g_2} = \sqrt {{g^2} + {a^2} + 2{\rm{a}}g\sin \alpha }$

$\Rightarrow g_2^2 = {g^2} + {a^2} + 2{\rm{a}}g\sin \alpha \,\,\,\,\,\left( 2 \right)$

Từ (1) và (2) ta có: $g_1^2 + g_2^2 = 2\left( {{g^2} + {a^2}} \right)$

$\Rightarrow \frac{1}{{T_1^4}} + \frac{1}{{T_2^4}} = \frac{2}{{{T^4}}} \Leftrightarrow \frac{1}{{2,{4^4}}} + \frac{1}{{1,{8^4}}} = \frac{2}{{{T^4}}} \Rightarrow T = 1,9984{\rm{s}}$