-
Câu hỏi:
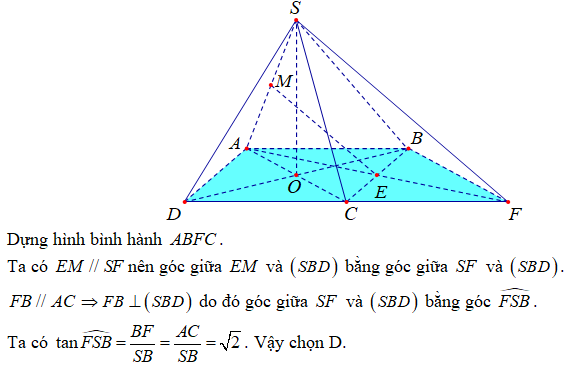
Cho hình chóp tứ giác đều \(S.ABCD\) có tất cả các cạnh bằng nhau. Gọi \(E, M\) lần lượt là trung điểm của các cạnh \(BC\) và \(SA\), \(\alpha \) là góc tạo bởi đường thẳng \(EM\) và mặt phẳng \((SBD)\). Giá trị của \(\tan \alpha \) bằng
- A. \(2\)
- B. \(\sqrt 3 \)
- C. \(1\)
- D. \(\sqrt 2 \)
Lời giải tham khảo:
Đáp án đúng: D
Câu hỏi này thuộc đề thi trắc nghiệm dưới đây, bấm vào Bắt đầu thi để làm toàn bài
Hướng dẫn Trắc nghiệm Online và Tích lũy điểm thưởng
CÂU HỎI KHÁC
- Cho khối chóp tứ giác đều có cạnh đáy bằng \(a\), cạnh bên bằng \(3a\). Tính thể tích \(V\) của khối chóp đã cho.
- Cho khối lăng trụ tam giác \(ABC.ABC\). Gọi \(M, N\) lần lượt là trung điểm của \(BB\) và \(CC\).
- Cho khối chóp S.ABCD có đáy là hình chữ nhật tính thể tích V của khối chóp đã cho
- Cho hình chóp \(S.ABC\) có đáy là tam giác vuông tại \(A; AB=a; AC=2a\).
- Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình thang với \(AD\,{\rm{//}}\,BC\) và \(AD = 2BC\).
- Cho hình chóp \(S.ABCD\) đáy là hình vuông cạnh \(a,{\rm{ }}SD = \frac{{a\sqrt {13} }}{2}\).
- Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O. AB=a. BAD=60, SO vuông góc (ABCD) tính thể tích khối chóp S.ABCD
- Cho hình chóp tứ giác đều có cạnh đáy bằng \(a\), cạnh bên bằng \(a\sqrt 2 \) (hình vẽ). Thể tích khối chóp là
- Cho khối lăng trụ \(ABC.ABC\), mặt \(\left( {ABBA} \right)\) có diện tích bằng 10.
- Cho hình chóp \(S.ABC\) có góc \(\widehat {ASB} = \widehat {BSC} = \widehat {CSA} = 60^\circ \), \(SA=2, SB=3, SC=6\).
- Cho khối chóp S.ABC có thể tích V nếu giữ nguyên chiều cao và tăng các cạnh đáy lên 3 lần thì thể tích khối chóp thu được là:
- Cho lăng trụ tam giác \(ABC.ABC\) có đáy là tam giác \(ABC\) đều cạnh bằng \)a\).
- Cho hình chóp (S.ABCD) có đáy (ABCD) là hình vuông cạnh (a) tính thể tích của khối chóp S.ABCD
- Cho lăng trụ tam giác \(ABC.ABC\) có đáy \(ABC\) là tam giác đều cạnh \(AB = 2a\sqrt 2 \).
- Một hình hộp chữ nhật \(ABCD.ABCD\) có ba kích thước là \(2 cm, 3 cm\) và \(6 cm\).
- Cho hình chóp tứ giác đều \(S.ABCD\) có tất cả các cạnh bằng nhau.
- Thể tích của khối chóp S.ABC bằng
- Cho hình lăng trụ tam giác đều \(ABC.
- Cho hình chóp \(S.ABCD\), đáy là hình vuông cạnh \(2a\).
- Góc giữa đường thẳng SC và mặt phẳng đáy ABCD là
- Cho hình chóp tứ giác đều có tất cả các cạnh bằng nhau, đường cao của một mặt bên là \(a\sqrt 3 \).
- Cho hình lập phương \(ABCD.ABCD\) có cạnh bằng \(a\). Gọi \(K\) là trung điểm của \(DD\).
- Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh 2a tính khoảng cách từ điểm S đến mặt phẳng (ABC)
- Cho khối lăng trụ đứng ABC.A'B'C' có đáy là tam giác cân tính thể tích V của khối lăng trụ đã cho.
- Cho khối chóp \(S.ABC\), gọi \(G\) là trọng tâm của tam giác \(ABC\). Tỉ số thể tích \(\frac{{{V_{S.ABC}}}}{{{V_{S.
- Cho hình lập phương \(ABCD.ABCD\) có cạnh bằng 1.
- Tính số đo góc giữa đường thẳng SB với mặt phẳng ABCD
- Khối bát diện đều có bao nhiêu mặt phẳng đối xứng?
- Cho lăng trụ tam giác đều \(ABC.ABC\) có cạnh đáy \(AB=a\), cạnh bên \(AA = \frac{{a\sqrt 2 }}{2}\).
- Cho hình chóp tam giác đều cạnh đáy bằng \(a\) và các mặt bên đều tạo với mặt phẳng đáy một góc bằng \(60^0\).
- Hình hộp chữ nhật có ba kích thước đôi một khác nhau có bao nhiêu mặt phẳng đối xứng?
- Cho khối chóp tam giác đều \(S.ABC\) có cạnh đáy bằng 4, chiều cao của khối chóp bằng chiều cao của tam giác đáy.
- Cho lăng trụ tam giác đều \(ABC.ABC\) có cạnh đáy bằng \(a\).
- Cho khối chóp \(S.ABCD\) có thể tích bằng \(\sqrt 3 {a^3}\).
- Cho hình chóp \(S.ABCD\) có \(ABCD\) là hình vuông cạnh \(a\), \(SA \bot \left( {ABCD} \right)\) và \(SA = a\sqrt 2 \).
- Cho lăng trụ đứng tam \(ABC.
- Cho hình chóp tứ giác \(S.
- Cho khối chóp \(S.ABCD\) có thể tích \(V\). Các điểm \(A, B, C\) tương ứng là trung điểm các cạnh \(SA, SB, SC\).
- Cho hình lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác vuông tại A diện tích của mặt cầu ngoại tiếp hình lăng trụ đã cho bằng
- Cho hình lăng trụ tam giác đều \(ABC.ABC\) có tất cả các cạnh bằng \(a\).