-
Câu hỏi:
Cho hình bình hành ABCD. Hai điểm M, N lần lượt là trung điểm của BC và AD. Tìm đẳng thức sai?
- A. ;
- B. ;
- C. ;
- D. .
Lời giải tham khảo:
Đáp án đúng: D
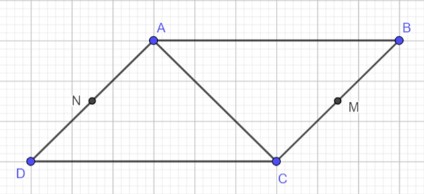
Ta xét từng đáp án:
Đáp án A: Theo quy tắc hình bình hành, ta có:
Tứ giác AMCN là hình bình hành ⇒ A đúng.
Đáp án B: Theo quy tắc hình bình hành, ta có:
Tứ giác ABCD là hình bình hành .
Mà từ đáp án A, ta có .
Do đó ta có ⇒ B đúng.
Đáp án C: Vì tứ giác AMCN là hình bình hành nên ta có và .
Do đó từ đáp án B, ta có ⇒ C đúng.
Đáp án D: Tứ giác ABCD là hình bình hành có AC và BD là hai đường chéo.
Do đó .
Vì vậy ⇒ D sai.
Đáp án đúng là: D
Câu hỏi này thuộc đề thi trắc nghiệm dưới đây, bấm vào Bắt đầu thi để làm toàn bài
Hướng dẫn Trắc nghiệm Online và Tích lũy điểm thưởng
CÂU HỎI KHÁC
- Trong các câu dưới đây, câu nào là mệnh đề?
- Đâu là mệnh đề chứa biến trong các câu dưới đây?
- Nếu cả hai MĐ: P ⇒ Q và Q ⇒ P đều sai thì ta suy ra điều gì?
- Chọn khẳng định đúng trong các khẳng định dưới đây?
- Trong các tập hợp dưới đây, tập hợp nào bằng nhau?
- Xác định M = A ∩ B trong TH A là tập hợp các tam giác đều, B là tập hợp các tam giác cân?
- Xác định M = A ∪ B trong trường hợp A = {x | x ∈ ℕ, x ⋮ 4 và x < 10}, B là tập hợp các số tự nhiên chia hết cho 3 và nhỏ hơn 12?
- Lớp 10E của trường có 30 học sinh thích môn Vật lí, 15 học sinh thích môn Hóa học và 10 học sinh thích cả môn Vật lí và Hóa học. Hỏi lớp 10A có bao nhiêu học sinh chỉ thích Vật lí hoặc chỉ thích Hóa học biết mỗi học sinh của lớp đều thích môn Vật lí hoặc Hoá học?
- Hình vẽ sau biểu diễn miền nghiệm (phần không bị gạch) của BPT bậc nhất hai ẩn nào?
- Chỉ ra câu sai trong các phát biểu dưới đây?
- Khi x = 2 và y ≥ 0 thì bất phương trình sau có mấy cặp nghiệm nguyên: 2x + y < 6?
- Bác An cần phải làm nến trong vòng không quá 8 giờ để bán. Nến loại A cần 30 phút để làm xong một cây, nến loại B cần 1 giờ để làm xong một cây. Gọi x, y lần lượt là số nến loại A, B bác An sẽ làm được. Hệ bất phương trình mô tả điều kiện của x và y là hệ bất phương trình nào sau đây?
- Cho hệ bất phương trình, điểm nào không thuộc miền nghiệm của hệ bất phương trình đã cho?
- Khoảng giá trị của x khi y = 1 trong hệ bất phương trình đã cho là
- Cho α là góc tù. Khẳng định nào đúng?
- Cho hai góc α và β (0° ≤ α, β ≤ 180°) với α + β = 90°. Giá trị biểu thức P = cosα.cosβ ‒ sinα.sinβ là?
- Giá trị của biểu thức: P = cos0° + cos1° + cos2° + ... + cos178° + cos179° + cos180° thuộc khoảng nào sau đây?
- Tam giác ABC có \(\widehat{A}={{105}^{0}};~\widehat{B}={{45}^{0}};~AC=10\]. Độ dài cạnh AB là?
- Tam giác ABC có \(AC=3\sqrt{3},~AB=3,~BC=6\). Số đo góc B là?
- Cho tam giác ABC nội tiếp đường tròn bán kính \(R,~ AB = R, ~AC=R\sqrt{2}\). Tính số đo của \(\widehat{A}\) biết \(\widehat{A}\) là góc tù?
- Diện tích của tam giác ABC với \(\widehat{A}\), AB = 20, AC = 10 là?
- Tam giác ABC có \(\widehat{A}\) = 68°12' , \(\widehat{B}\)= 34°44', AB = 117. Độ dài cạnh AC là khoảng?
- Tam giác ABC có góc A nhọn, AB = 5, AC = 8, diện tích bằng 12. Độ dài cạnh BC là khoảng?
- Để đo chiều cao từ mặt đất đến đỉnh cột cờ của một kỳ đài trước Ngọ Môn (Đại Nội – Huế), người ta cắm hai cọc AM và BN cao 1,5 mét so với mặt đất. Chiều cao của cột cờ (làm tròn kết quả đến chữ số thập phân thứ hai) là?
- Cho hai vectơ không cùng phương a và b. Mệnh đề nào sau đây đúng?
- Cho hình vuông ABCD, khẳng định nào đúng?
- Cho 5 điểm M, N, P, Q, R. Tính tổng vecto MN + PQ + RN + NP + QR?
- Cho tam giác ABC đều có độ dài cạnh bằng a. Độ dài vecto AB + BC bằng?
- Cho hình bình hành ABCD. 2 điểm M, N lần lượt là trung điểm của BC và AD. Tìm đẳng thức sai?
- Cho 2 lực \(F_1\) và \(F_1\) có cùng điểm đặt O và vuông góc với nhau. Cường độ của hai lực vecto \(F_1\) và \(F_1\) lần lượt là 80N và 60N. Cường độ tổng hợp lực của hai lực đó là?
- Cho ba điểm phân biệt A, B, C. Nếu \(\overrightarrow{AB}=-3\overrightarrow{AC}\) thì đẳng thức nào dưới đây đúng?
- Cho tam giác ABC. Gọi I là trung điểm AB. Tìm điểm M thỏa mãn hệ thức \(\overrightarrow{MA}+\overrightarrow{MB}+2\overrightarrow{MC}=\vec{0}\)?
- Cho hình bình hành ABCD, điểm M thỏa mãn \(4\overrightarrow{AM}=\overrightarrow{AB}+\overrightarrow{AD}+\overrightarrow{AC}\). Xác định vị trí điểm M?
- Cho tam giác ABC và một điểm M tùy ý. Cho \(\overrightarrow{v}=\overrightarrow{MA}+\overrightarrow{MB}+2\overrightarrow{MC}\). Hãy xác định vị trí của điểm D sao cho \(\overrightarrow{CD}=\overrightarrow{v}\)?
- Tìm m để hàm số \(y = \frac{x}{x-m}\) xác định trên khoảng (0; 5)?
- Cho hàm số y = f(x) có đồ thị như hình vẽ: Khẳng định nào đúng?
- Hàm số \(y = 2x^{2} – 4x + 1\) đồng biến và nghịch biến trên khoảng nào?
- Hàm số nào dưới đây có đỉnh S(1; 0)?
- Cho hình chữ nhật ABCD có \(AB = \sqrt{2},~ AD = 1\). Tính góc giữa hai vectơ AC và BD?
- Cho tam giác đều ABC có cạnh a. Tính tích vô hướng của hai vecto AB.AC?







